题目内容

在空间四边形ABCD中，求证：
AB
•
CD
+
AC
•
DB
+
AD
•
BC
=0．
分析：证法一：把
AB
拆成
AC
+
CB
后重组，根据平面向量数量积的运算律进行运算求解．
证法二：利用数形结合，将
DA
，
DB
，
DC
设为基底向量
a
、
b
、
c
，利用向量的几何意义表示出各未知向量，进而求解．
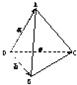解答：精英家教网证法一：把
AB
拆成
AC
+
CB
后重组，
AB
•
CD
+
AC
•
DB
+
AD
•
BC
=（
AC
+
CB
）•
CD
+
AC
•
DB
+
AD
•
BC
=
AC
•
CD
+
CB
•
CD
+
AC
•
DB
+
AD
•
BC
=
AC
•（
CD
+
DB
）+
CB
•（
CD
+
DA
）=
AC
•
CB
+
CB
•
CA
=
CB
•（
AC
+
CA
）=
CB
•0=0．
证法二：如图，设a=
DA
，b=
DB
，c=
DC
，则
AB
•
CD
+
AC
•
DB
+
AD
•
BC
=（b-a）•（-c）+（c-a）•b+
（-a）•（c-b）=-b•c+a•c+c•b-a•b-a•c+a•b=0．
点评：本题考查了向量数量积的运算，是高考考查的重点，其中证法二利用了平面向量基本定理和数形结合的思想，有效地简化了运算．
练习册系列答案
相关题目
8、在空间四边形ABCD的各边AB，BC，CD，DA上依次取点E，F，G，H，若EH、FG所在直线相交于点P，则（　　）
在空间四边形ABCD的边AB，BC，CD，DA上分别取E，F，G，H使
AE
EB
=
AH
HD
=1，
CF
FB
=
CG
GD
=
1
2
，则（　　）
在空间四边形ABCD中，连接AC、BD，若△BCD是正三角形，且E为其中心，则
AB
+
1
2
BC
-
3
2
DE
-
AD
化简后的结果为（　　）
A、
AB
B、2
BD
C、
0
D、2
DE
（2011•顺义区一模）如图，已知在空间四边形ABCD中，AB=AC=DB=DC，E为BC的中点．
（Ⅰ）求证：平面ADE⊥平面ABC；
（Ⅱ）若AB=5，BC=6，AD=4，求几何体ABCD的体积；
（Ⅲ）在（Ⅱ）的条件下，若G为△ABD的重心，试问在线段BC上是否存在点F，使GF∥平面ADE？若存在，请指出点F在BC上的位置，若不存在，请说明理由．
在空间四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA的中点．若AC=BD=a，若四边形EFGH的面积为
3
8
a2，则异面直线AC与BD所成的角为（　　）
A、30°B、60°
C、120°D、60°或120°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网