题目内容
设函数f(x)的定义域为R,若存在常数m>0使|f(x)|≤m|x|对一切实数x均成立,则称f(x)为°F函数.给出下列函数:
A. B.
B.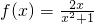 C.
C. D.f(x)是定义在R上的奇函数,且对一切实数x1,x2均有|f(x1)-f(x2)|≤a|x1-x2|(a>0);其中是°F函数的序号________.
D.f(x)是定义在R上的奇函数,且对一切实数x1,x2均有|f(x1)-f(x2)|≤a|x1-x2|(a>0);其中是°F函数的序号________.
B,D
分析:对任意x∈R,存在常数m>0使|f(x)|≤m|x|对一切实数x均成立,即对任意x∈R,存在正数m,都有 m≥ 成立
成立
对各选项,对照定义,一一判断,即可得出结论.
解答:对于A,∵ =
= =
=
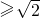 ,∴
,∴ ,对照定义,可知不满足题意;
,对照定义,可知不满足题意;
对于B,∵ =
= ,∴存在正数m,都有 m≥
,∴存在正数m,都有 m≥ 成立,故B满足题意;
成立,故B满足题意;
对于C, ,不难发现:因为x→0时,
,不难发现:因为x→0时, →∞,所以不存在常数m>0,使|f(x)|≤m|x|对一切实数x均成立,故C不满足题意;
→∞,所以不存在常数m>0,使|f(x)|≤m|x|对一切实数x均成立,故C不满足题意;
对于D,f(x)是定义在实数集R上的奇函数,故f(0)=0,因而由对一切实数x1,x2均有|f(x1)-f(x2)|≤a|x1-x2|(a>0),当x2=0时,得到|f(x1)|≤a|x1|成立,即|f(x)|≤a|x|成立,所以存在m≥a>0,使|f(x)|≤m|x|对一切实数x均成立,符合题意.
故答案为:B,D.
点评:本题重点考查了函数的最值及其性质,对选支逐个加以分析变形,利用函数、不等式的进行检验,方可得出正确结论.深刻理解题中°F函数的定义,用不等式的性质加以处理,找出不等式恒成立的条件再进行判断,是解决本题的关键所在.
分析:对任意x∈R,存在常数m>0使|f(x)|≤m|x|对一切实数x均成立,即对任意x∈R,存在正数m,都有 m≥
 成立
成立对各选项,对照定义,一一判断,即可得出结论.
解答:对于A,∵
 =
= =
=
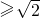 ,∴
,∴ ,对照定义,可知不满足题意;
,对照定义,可知不满足题意;对于B,∵
 =
= ,∴存在正数m,都有 m≥
,∴存在正数m,都有 m≥ 成立,故B满足题意;
成立,故B满足题意;对于C,
 ,不难发现:因为x→0时,
,不难发现:因为x→0时, →∞,所以不存在常数m>0,使|f(x)|≤m|x|对一切实数x均成立,故C不满足题意;
→∞,所以不存在常数m>0,使|f(x)|≤m|x|对一切实数x均成立,故C不满足题意;对于D,f(x)是定义在实数集R上的奇函数,故f(0)=0,因而由对一切实数x1,x2均有|f(x1)-f(x2)|≤a|x1-x2|(a>0),当x2=0时,得到|f(x1)|≤a|x1|成立,即|f(x)|≤a|x|成立,所以存在m≥a>0,使|f(x)|≤m|x|对一切实数x均成立,符合题意.
故答案为:B,D.
点评:本题重点考查了函数的最值及其性质,对选支逐个加以分析变形,利用函数、不等式的进行检验,方可得出正确结论.深刻理解题中°F函数的定义,用不等式的性质加以处理,找出不等式恒成立的条件再进行判断,是解决本题的关键所在.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 )与b=f(
)与b=f( )的大小关系为________.
)的大小关系为________. )与b=f(
)与b=f( )的大小关系为 .
)的大小关系为 . )与b=f(
)与b=f( )的大小关系为( ).
)的大小关系为( ).