题目内容
已知函数f(x)=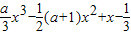 (a∈R).
(a∈R).(1)若a<0,求函数f(x)的极值;
(2)是否存在实数a使得函数f(x)在区间[0,2]上有两个零点,若存在,求出a的取值范围;若不存在,说明理由.
【答案】分析:(1)对f(x)进行求导,求出极值点,列出表格,进而求函数f(x)的极值;
(2)求出f(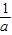 ),f(1),f(2)的值,讨论
),f(1),f(2)的值,讨论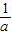 与1,2值的大小,利用零点定理进行判断;
与1,2值的大小,利用零点定理进行判断;
解答:解:(1)f′(x)=ax2-(a+1)x+1=a(x-1)(x-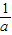 )
)
∵a<0,∴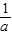 <1,
<1,
∴f(x)极大值=f(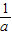 )=
)=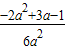 ,f(x)极大值=f(1)=-
,f(x)极大值=f(1)=- (a-1)
(a-1)
(2)f(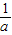 )=
)=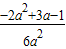 =
=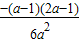 ,f(1)=-
,f(1)=- (a-1)
(a-1)
f(2)= (2a-1),f(0)=-
(2a-1),f(0)=- <0,
<0,
①当a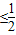 时f(x)在[0,1]上为增函数,在[1,2]上为减函数,f(0)=
时f(x)在[0,1]上为增函数,在[1,2]上为减函数,f(0)=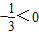 ,
,
f(1)=- (a-1)>0,f(2)=
(a-1)>0,f(2)= (2a-1)≤0,所以f(x)在区间[0,1],(1,2]上各有一个零点,即在[0,2]上有两个零点;
(2a-1)≤0,所以f(x)在区间[0,1],(1,2]上各有一个零点,即在[0,2]上有两个零点;
当 <a≤1时,f(x)在[0,1]上为增函数,在(1,
<a≤1时,f(x)在[0,1]上为增函数,在(1,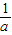 )上为减函数,(
)上为减函数,(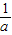 ,2)上为增函数,f(0)=
,2)上为增函数,f(0)=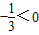 ,
,
f(1)=- (a-1)>0,f(
(a-1)>0,f(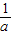 )=
)=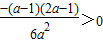 ,f(2)=
,f(2)= (2a-1)>0,
(2a-1)>0,
所以f(x)只在区间[0,1]上有一个零点,故在[0,2]上只有一个零点;
③当a>1时,f(x)在[0,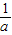 ]上为增函数,在(
]上为增函数,在(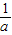 ,1)上为减函数,(1,2)上为增函数,f(0)=-
,1)上为减函数,(1,2)上为增函数,f(0)=- <0,f(
<0,f(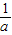 )=
)=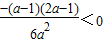 ,f(1)=-
,f(1)=- (a-1)<0,f(2)=
(a-1)<0,f(2)= (2a-1)>0,
(2a-1)>0,
,所以f(x)只在区间(1,2)上有一个零点,故在[0,2]上只有一个零点;
故存在实数a,当a≤ 时,函数f(x)在区间[0,2]上有两个零点;
时,函数f(x)在区间[0,2]上有两个零点;
点评:本题考查利用导数研究函数的单调性,考查存在性问题,突出考查函数的零点定理,分类讨论数学思想及综合分析与运算的能力,属于难题.
(2)求出f(
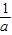 ),f(1),f(2)的值,讨论
),f(1),f(2)的值,讨论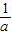 与1,2值的大小,利用零点定理进行判断;
与1,2值的大小,利用零点定理进行判断;解答:解:(1)f′(x)=ax2-(a+1)x+1=a(x-1)(x-
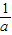 )
)∵a<0,∴
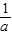 <1,
<1,(-∞,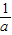 ) ) | 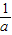 | (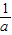 ,1) ,1) | 1 | (1,+∞) | |
| f′(x) | - | + | - | ||
| f(x) | 递减 | 极小值 | 递增 | 极大值 | 递减 |
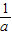 )=
)=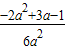 ,f(x)极大值=f(1)=-
,f(x)极大值=f(1)=- (a-1)
(a-1)(2)f(
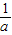 )=
)=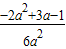 =
=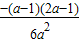 ,f(1)=-
,f(1)=- (a-1)
(a-1)f(2)=
 (2a-1),f(0)=-
(2a-1),f(0)=- <0,
<0,①当a
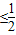 时f(x)在[0,1]上为增函数,在[1,2]上为减函数,f(0)=
时f(x)在[0,1]上为增函数,在[1,2]上为减函数,f(0)=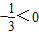 ,
,f(1)=-
 (a-1)>0,f(2)=
(a-1)>0,f(2)= (2a-1)≤0,所以f(x)在区间[0,1],(1,2]上各有一个零点,即在[0,2]上有两个零点;
(2a-1)≤0,所以f(x)在区间[0,1],(1,2]上各有一个零点,即在[0,2]上有两个零点;当
 <a≤1时,f(x)在[0,1]上为增函数,在(1,
<a≤1时,f(x)在[0,1]上为增函数,在(1,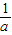 )上为减函数,(
)上为减函数,(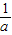 ,2)上为增函数,f(0)=
,2)上为增函数,f(0)=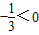 ,
,f(1)=-
 (a-1)>0,f(
(a-1)>0,f(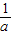 )=
)=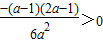 ,f(2)=
,f(2)= (2a-1)>0,
(2a-1)>0,所以f(x)只在区间[0,1]上有一个零点,故在[0,2]上只有一个零点;
③当a>1时,f(x)在[0,
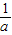 ]上为增函数,在(
]上为增函数,在(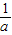 ,1)上为减函数,(1,2)上为增函数,f(0)=-
,1)上为减函数,(1,2)上为增函数,f(0)=- <0,f(
<0,f(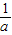 )=
)=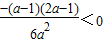 ,f(1)=-
,f(1)=- (a-1)<0,f(2)=
(a-1)<0,f(2)= (2a-1)>0,
(2a-1)>0,,所以f(x)只在区间(1,2)上有一个零点,故在[0,2]上只有一个零点;
故存在实数a,当a≤
 时,函数f(x)在区间[0,2]上有两个零点;
时,函数f(x)在区间[0,2]上有两个零点;点评:本题考查利用导数研究函数的单调性,考查存在性问题,突出考查函数的零点定理,分类讨论数学思想及综合分析与运算的能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|