题目内容
已知圆M过两点C(1,-1),D(-1,1),,且圆心M在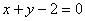 上.
上.
(1)求圆M的方程;
(2)设p是直线3x+4y+8=0上的动点,PA,PB是圆M的两条切线,A,B为切点,求四边形PAMB面积的最小值.
解:(1)设圆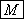 的方程为:(x-a)2+(y-b)2=r2(r>0).
的方程为:(x-a)2+(y-b)2=r2(r>0).
根据题意,得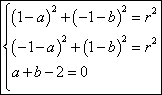 ﹍﹍﹍﹍﹍﹍﹍3分
﹍﹍﹍﹍﹍﹍﹍3分
解得a=b=1,r=2, ﹍﹍﹍﹍﹍﹍﹍5分
故所求圆M的方程为(x-1)2+(y-1)2=4. ﹍﹍﹍﹍﹍﹍﹍6分
(2)因为四边形PAMB的面积S=S△PAM+S△PBM=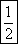 |AM|·|PA|+
|AM|·|PA|+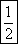 |BM|·|PB|,
|BM|·|PB|,
又|AM|=|BM|=2,|PA|=|PB|, 所以S=2|PA|, ﹍﹍﹍﹍﹍﹍﹍8分
而|PA|=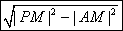 =
=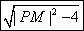 , 即S=2
, 即S=2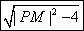 .
.
因此要求S的最小值,只需求|PM|的最小值即可,即在直线3x+4y+8=0上找一点P,
使得|PM|的值最小
所以|PM|min=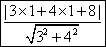 =3, ﹍﹍﹍﹍﹍﹍﹍10分
=3, ﹍﹍﹍﹍﹍﹍﹍10分
所以四边形PAMB面积的最小值为S=2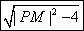 =2
=2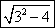 =2
=2 .
.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 作一直线与椭圆
作一直线与椭圆 相交于
相交于 两点,若
两点,若 点恰好为弦
点恰好为弦 的中点,则
的中点,则 满足
满足 则
则 的取值范围是
的取值范围是 
 或
或

 或
或
 是两条不同的直线,
是两条不同的直线,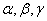 是三个不同的
是三个不同的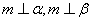 ,则
,则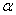 ∥
∥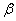
 ,
,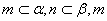 ∥
∥ ,则
,则 ,则( )
,则( ) 的定义域为
的定义域为 ,若
,若 ,使
,使 上值域为
上值域为 为闭函数,则
为闭函数,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 的一条渐近线方程为y=
的一条渐近线方程为y= x,则双曲线的离心率为( )
x,则双曲线的离心率为( ) B.
B.  C.
C.  D.
D. 

 的左焦点,
的左焦点,
 是双曲线右支上的动点,则
是双曲线右支上的动点,则
 的最小值为 .
的最小值为 .