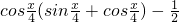题目内容

设函数y=f（x）满足对任意的x∈R，f（x）≥0且f²（x+1）+f²（x）=9．已知当x∈[0，1]时，有f（x）=2-|4x-2|，则 $数学公式$ 的值为________．

$\text{[math]}$
分析：由条件求得可得 f（x+2）=f（x），故函数是周期为2的周期函数，可得 $\text{[math]}$ =f（- $\text{[math]}$ ），先求得f（ $\text{[math]}$ ）的值，
根据f²（x+1）+f²（x）=9，即可求得f（- $\text{[math]}$ ）的值，从而求得 $\text{[math]}$ 的值．
解答：∵f²（x+1）+f²（x）=9，即 f²（x+1）=9-f²（x），
∴f²（x+2）=9-f²（x+1），化简可得 f²（x+2）=9-[9-f²（x）]=f²（x）．
再由函数y=f（x）满足对任意的x∈R，f（x）≥0，可得 f（x+2）=f（x），故函数是周期为2的周期函数．
∴ $\text{[math]}$ =f（336- $\text{[math]}$ ）=f（- $\text{[math]}$ ）．
又 f²（- $\text{[math]}$ ）=9- $\text{[math]}$ =9-f²（ $\text{[math]}$ ），
再由当x∈[0，1]时，有f（x）=2-|4x-2|，可得f（ $\text{[math]}$ ）=2-|4× $\text{[math]}$ -2|=2，
故 f²（- $\text{[math]}$ ）=9-f²（ $\text{[math]}$ ）=9-4=5，故f（- $\text{[math]}$ ）= $\text{[math]}$ ，
故 $\text{[math]}$ =f（- $\text{[math]}$ ）= $\text{[math]}$ ，
故答案为 $\text{[math]}$ ．
点评：本题主要考查了抽象函数的求值，同时考查了函数的周期性，属于中档题．