题目内容
已知函数
，判断f（x）的奇偶性并且证明．
【答案】分析：由于此函数是由两个奇函数的和构成的，可判断其为奇函数，再利用奇函数的定义证明：先证明定义域关于原点对称，在证明f（-x）=-f（x）即可
解答：解：f（x）是奇函数
证明：f（x）的定义域是（-∞，0）∪（0，+∞），定义域关于原点对称
在f（x）的定义域内任取一个x，则有
所以，f（x）是奇函数
点评：本题考查了奇函数的定义，判断函数奇偶性的方法，奇函数的证明方法．
解答：解：f（x）是奇函数
证明：f（x）的定义域是（-∞，0）∪（0，+∞），定义域关于原点对称
在f（x）的定义域内任取一个x，则有
所以，f（x）是奇函数
点评：本题考查了奇函数的定义，判断函数奇偶性的方法，奇函数的证明方法．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
．
有解，求m的取值范围；
，
，对任意
都有意义，求
的取值范围．
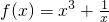，判断f（x）的奇偶性并且证明．
，判断f（x）的奇偶性并且证明．
，判断f（x）的奇偶性并且证明．