Question

在抛物线y²=4x上求一点,使它到直线x+y=-5的距离最短.

Answer 1

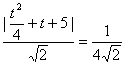解法一:设抛物线上任一点A(,t),点A到直线x+y=-5的距离为d=（t²+4t+20）=［(t+2)²+16］.

∵t∈R,∴取t=-2得d_最小=2.

解法二:把直线l:x+y=-5向上平移到l′:x+y=m,使l′与抛物线相切,所求最小值就是平行线l与l′间的距离.

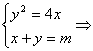y²+4y-4m=0,

Δ=16+16m=0.∴m=-1.

∴l′:x+y=-1.

∴d_最小=.