题目内容
12．
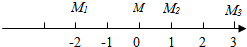三台机器人位于同一直线上（如图所示），它们所生产的零件必须逐一送到一个检验台上，经检验合格后，才能送到下一道工序继续加工，已知机器人M1的工作效率是机器人M2的2倍，机器人M2的工作效率是机器人M3的3倍，问检验台放何处最好？（即各机器人到检验台所走距离的总和最小）
分析 设检验台应该设在x轴上的M处，M点表示的数为x，根据数轴上两点之间的距离的表示方法得到移动的距离总和S=6×|x+2|+3×|x-1|+1×|x-3|，然后分类讨论：当x≤-2时或当-2＜x＜1时或当1≤x≤3时或当x＞3时，分别去绝对值得到各范围内S的最小值，然后确定M点的位置．
解答 解：设检验台应该设在x轴上的M处，M点表示的数为x，
根据题意设移动的距离总和S=6×|x+2|+3×|x-1|+1×|x-3|
=6|x+2|+3|x-1|+|x-3|，
当x≤-2时，S=-6x-12-3x+3-x+3=-10x-6，此时x=-2时，S的值最小为14；
当-2＜x＜1时，S=6x+12-3x+3-x+3=2x+18，S没有值最小值；
当1≤x≤3时，S=6x+12+3x-3-x+3=8x+12，此时x=1时，S的值最小为20；
当x＞3时，S=6x+12+3x-3+x-3=10x+6，此时S没有最小值．
综上可得，x=-2处，各机器人到检验台所走距离的总和最小，
所以检验台应该设在x轴上的M1处，才能使移动的距离之和最小．
点评 本题考查了绝对值的含义：若a＞0，则|a|=a；若a=0，则|a|=0；若a＜0，则|a|=-a．也考查了实际应用与分类讨论的思想．
练习册系列答案
相关题目
20．$\sqrt{1-co{s}^{2}\frac{π}{5}}$=（ ）
| A． | sin$\frac{π}{5}$ | B． | cos$\frac{π}{5}$ | C． | -sin$\frac{π}{5}$ | D． | -cos$\frac{π}{5}$ |