题目内容
等差数列{an}的前16项和为640,前16项中偶数项和与奇数项和之比为22:18,则公差d,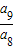 的值分别是 .
的值分别是 .
【答案】分析:设出奇次项与偶次项,根据之和为640,之比为22:18,求出奇次项与偶次项,利用等差数列的性质求出公差d的值,利用等差数列的性质及求和公式得出所求第9项与第8项之比为偶次项之和与奇次项之和的比,求出即可.
解答:解:设S奇=a1+a3+…+a15,S偶=a2+a4+…+a16,
∵ ,
,
解得:S奇=288,S偶=352,
则有S偶-S奇=(a2-a1)+(a4-a3)+…+(a16-a15)=8d=352-288,
解得:d=8,
则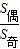 =
=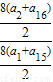 =
=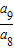 =
=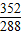 =
=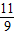 .
.
故选D
点评:此题考查了等差数列的性质,熟练掌握等差数列的性质是解本题的关键.
解答:解:设S奇=a1+a3+…+a15,S偶=a2+a4+…+a16,
∵
 ,
,解得:S奇=288,S偶=352,
则有S偶-S奇=(a2-a1)+(a4-a3)+…+(a16-a15)=8d=352-288,
解得:d=8,
则
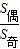 =
=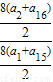 =
=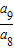 =
=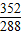 =
=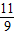 .
.故选D
点评:此题考查了等差数列的性质,熟练掌握等差数列的性质是解本题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
设等差数列{an}的前n项和为Sn,则a5+a6>0是S8≥S2的( )
| A、充分而不必要条件 | B、必要而不充分条件 | C、充分必要条件 | D、既不充分也不必要条件 |