题目内容
(本小题满分12分)
如图,函数f1(x)=A sin(wx+j)(A>0,w>0,|j|<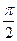 )的一段图象,过点(0,1).(1)求函数f1(x)的解析式;(2)将函数y=f1(x)的图象按向量
)的一段图象,过点(0,1).(1)求函数f1(x)的解析式;(2)将函数y=f1(x)的图象按向量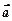 =
=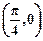 平移,得到函数y=f2(x),求y=f1(x)+f2(x)的最大值,并求此时自变量x的集合.
平移,得到函数y=f2(x),求y=f1(x)+f2(x)的最大值,并求此时自变量x的集合.
如图,函数f1(x)=A sin(wx+j)(A>0,w>0,|j|<
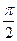 )的一段图象,过点(0,1).(1)求函数f1(x)的解析式;(2)将函数y=f1(x)的图象按向量
)的一段图象,过点(0,1).(1)求函数f1(x)的解析式;(2)将函数y=f1(x)的图象按向量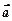 =
=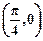 平移,得到函数y=f2(x),求y=f1(x)+f2(x)的最大值,并求此时自变量x的集合.
平移,得到函数y=f2(x),求y=f1(x)+f2(x)的最大值,并求此时自变量x的集合.(1)2sin(2x+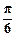 ) (2)
) (2)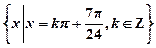
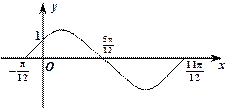
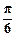 ) (2)
) (2)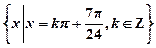
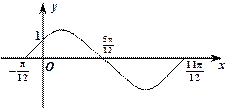
(1)由图知:T=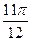 -(-
-(- )=
)=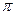 ,
,
于是w=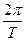 =2.……………2分
=2.……………2分
设f1(x)=A sin(2x+j),
将函数f(x)=A sin2x的图象向左平移 ,
,
得f1(x)=A sin(2x+j)的图象,······················································· 3分
则j=2× =
=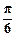 ,
,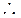 f1(x)=A sin(2x+
f1(x)=A sin(2x+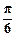 ).······································ 4分
).······································ 4分
将(0,1)代入f1(x)=A sin(2x+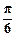 ),易得A=2.····························· 6分
),易得A=2.····························· 6分
故f1(x)=2sin(2x+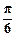 );·································································· 7分
);·································································· 7分
(2)依题意:f2(x)=2sin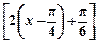 =-2cos
=-2cos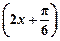 ,······················ 8分
,······················ 8分
∴y=2sin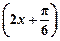 -2cos
-2cos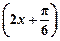 =2
=2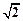 sin
sin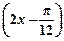 .····························· 11分
.····························· 11分
当2x- =2
=2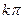 +
+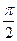 ,即x=
,即x=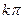 +
+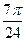 ,k∈
,k∈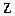 时,ymax=2
时,ymax=2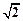 .
.
此时,x的取值集合为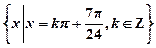 .………… 12分
.………… 12分
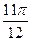 -(-
-(- )=
)=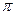 ,
,于是w=
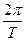 =2.……………2分
=2.……………2分设f1(x)=A sin(2x+j),
将函数f(x)=A sin2x的图象向左平移
 ,
,得f1(x)=A sin(2x+j)的图象,······················································· 3分
则j=2×
 =
=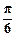 ,
,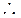 f1(x)=A sin(2x+
f1(x)=A sin(2x+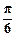 ).······································ 4分
).······································ 4分将(0,1)代入f1(x)=A sin(2x+
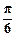 ),易得A=2.····························· 6分
),易得A=2.····························· 6分故f1(x)=2sin(2x+
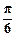 );·································································· 7分
);·································································· 7分(2)依题意:f2(x)=2sin
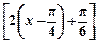 =-2cos
=-2cos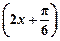 ,······················ 8分
,······················ 8分∴y=2sin
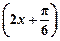 -2cos
-2cos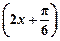 =2
=2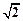 sin
sin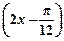 .····························· 11分
.····························· 11分当2x-
 =2
=2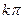 +
+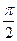 ,即x=
,即x=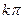 +
+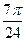 ,k∈
,k∈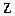 时,ymax=2
时,ymax=2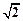 .
.此时,x的取值集合为
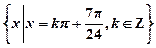 .………… 12分
.………… 12分
练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
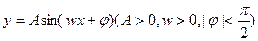 的图像上相邻的最高点与最低点的坐标分别为
的图像上相邻的最高点与最低点的坐标分别为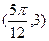 和
和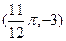 。 (1)求出
。 (1)求出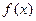 的解析式。(2)找出
的解析式。(2)找出 cosx+a=0在(0, 2π)内有相异二解α、β.
cosx+a=0在(0, 2π)内有相异二解α、β. 已知函数
已知函数 的最大值为
的最大值为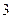 ,其中
,其中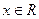 .(Ⅰ)求
.(Ⅰ)求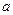 的值(Ⅱ)如果
的值(Ⅱ)如果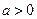 ,求函数
,求函数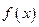 的对称中心;
的对称中心; 中,既是偶函数又是周期函数的个数是( )
中,既是偶函数又是周期函数的个数是( )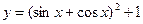 的最小正周期是
的最小正周期是



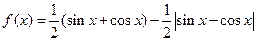 ,则
,则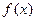 的值域是( )
的值域是( )



 的图象,经过平移变换与伸缩变换后,可得函数
的图象,经过平移变换与伸缩变换后,可得函数 的图象.下面说法不正确的是.( )
的图象.下面说法不正确的是.( ) 个单位,再向下平移1个单位,后纵坐标伸长到原来的2倍(横坐标不变)
个单位,再向下平移1个单位,后纵坐标伸长到原来的2倍(横坐标不变) 个单位,再向下平移1个单位,然后横坐标伸长到原来的2倍(纵坐标不变),后纵坐标伸长到原来的2倍(横坐标不变)
个单位,再向下平移1个单位,然后横坐标伸长到原来的2倍(纵坐标不变),后纵坐标伸长到原来的2倍(横坐标不变)