题目内容
某租赁公司出租同一型号的设备40套,当每套月租金为270元时,恰好全部租出,在此基础上,每套月租金每增加10元,就少租出1套设备,而未租出的设备每月需支付各种费用每套20元,设每套设备实际月租金为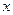
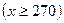 元,月收益为
元,月收益为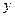 元(总收益=设备租金收入—未租出设备支出费用)。
元(总收益=设备租金收入—未租出设备支出费用)。
⑴求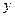 与
与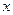 的函数关系式;
的函数关系式;
⑵当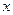 为何值时,月收益最大?最大月收益是多少?
为何值时,月收益最大?最大月收益是多少?
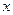
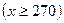 元,月收益为
元,月收益为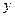 元(总收益=设备租金收入—未租出设备支出费用)。
元(总收益=设备租金收入—未租出设备支出费用)。⑴求
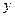 与
与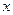 的函数关系式;
的函数关系式;⑵当
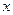 为何值时,月收益最大?最大月收益是多少?
为何值时,月收益最大?最大月收益是多少? 解⑴每套设备实际月租金为
解⑴每套设备实际月租金为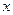
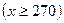 元时,未租出的设备为
元时,未租出的设备为 套,则未租出设备支出费用为
套,则未租出设备支出费用为 元;租出的设备为
元;租出的设备为 套,则设备租金收入为
套,则设备租金收入为 元。
元。所以月收益
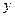 与
与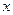 的函数关系式是
的函数关系式是 ;……………6分
;……………6分⑵由⑴得
 ,所以当
,所以当 时,
时,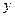 取得最大值为
取得最大值为 ,但是当每套月租金为325元是,租出设备的套数为34.5,而34.5不是整数,不符合题意,故租出的设备应为34套或35套,即当每套月租金为330元(租出34套)或每套租金为320元(租出35套)时,租赁公司的月收益最大,最大收益为均为11100元。12分
,但是当每套月租金为325元是,租出设备的套数为34.5,而34.5不是整数,不符合题意,故租出的设备应为34套或35套,即当每套月租金为330元(租出34套)或每套租金为320元(租出35套)时,租赁公司的月收益最大,最大收益为均为11100元。12分略

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案
相关题目
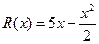 (万元)
(万元)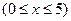 ,其中
,其中
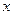 是产品售出的数量(单位:百台)
是产品售出的数量(单位:百台)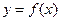 的定义域为
的定义域为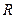 ,当
,当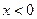 时,
时,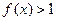 ,且对任意的实数
,且对任意的实数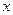 ,
,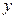
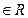 ,
,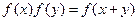 恒成立.若数列{
恒成立.若数列{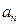 }满足
}满足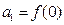 ,且
,且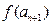 =
=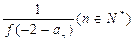 ,
,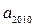 的值为
的值为  的定义域是 ( )
的定义域是 ( )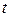
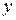




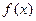 的定义域为D,若存在非零实数
的定义域为D,若存在非零实数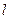 使得对于任意
使得对于任意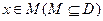 ,有
,有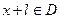 ,且
,且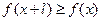 ,则称
,则称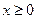 时,
时,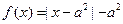 ,且
,且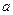 的取值范围是 ( )
的取值范围是 ( )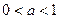
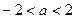
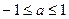
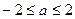
 是
是 的两实根;
的两实根; 是
是 的两实根。若
的两实根。若 ,则实数
,则实数 的取值范围是 ;
的取值范围是 ; ),定义运算"⊙"为(a,b)⊙(c,d)=(a+c,bd),且(x,1)⊙(2,y)
),定义运算"⊙"为(a,b)⊙(c,d)=(a+c,bd),且(x,1)⊙(2,y) 2,1)
2,1) ,则方程
,则方程 的实根个数为
的实根个数为 ,且
,且
 ,则
,则 ( ▲ )
( ▲ )
