题目内容
若集合M={y|y=2x},N={y|y=x2},则下列结论①M∩N={2,4};②M∩N={4,16};③M∪N=[0,+∞);④M=N;⑤M?N,其中正确的结论的序号为________.
③⑤
分析:根据指数函数的图象和性质,可以求出集合M,根据二次函数的图象和性质,可以求出集合N,进而逐一分析五个结论的正误,可得答案.
解答:∵集合M={y|y=2x}=(0,+∞)
集合N={y|y=x2}=[0,+∞)
则M∩N=M≠{2,4},故①错误;
则M∩N=M≠{4,16},故②错误;
M∪N=N=[0,+∞),故③正确;
M≠N,故④错误;
M⊆N,且M≠N,故M?N,故⑤正确;
故答案为:③⑤
点评:本题考查的知识点是子集与交集,并集运算的转化,熟练掌握基本初等函数的图象和性质,求出集合M,N是解答的关键.
分析:根据指数函数的图象和性质,可以求出集合M,根据二次函数的图象和性质,可以求出集合N,进而逐一分析五个结论的正误,可得答案.
解答:∵集合M={y|y=2x}=(0,+∞)
集合N={y|y=x2}=[0,+∞)
则M∩N=M≠{2,4},故①错误;
则M∩N=M≠{4,16},故②错误;
M∪N=N=[0,+∞),故③正确;
M≠N,故④错误;
M⊆N,且M≠N,故M?N,故⑤正确;
故答案为:③⑤
点评:本题考查的知识点是子集与交集,并集运算的转化,熟练掌握基本初等函数的图象和性质,求出集合M,N是解答的关键.

练习册系列答案
相关题目
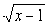 },则M∩P等于 ( )
},则M∩P等于 ( ) ,则M∩P=( )
,则M∩P=( ) ,则M∩P=( )
,则M∩P=( ) ,则M∩P=( )
,则M∩P=( )