题目内容
已知函数f（x）=（1+cotx）sin2x﹣2sin（x+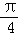
）sin（x﹣
）．
（1）若tanα=2，求f（α）；
（2）若x∈[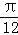
，
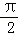]，求f（x）的取值范围．
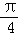）sin（x﹣）．（1）若tanα=2，求f（α）；
（2）若x∈[
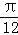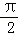，]，求f（x）的取值范围．解：（1）∵f（x）=（1+cotx）sin2x﹣2sin（x+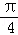
）sin（x﹣
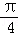）=sin2x+sinxcosx+cos2x=
+
=
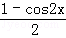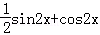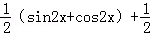
∵tanα=2，∴sin2α=2sinαcosα=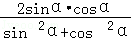
=
=
，
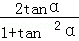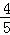cos2α=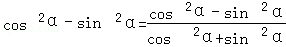
=
=
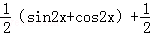
由tanα=2得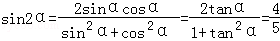
，
，
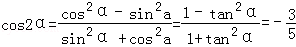所以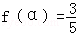
．
（2）由（1）得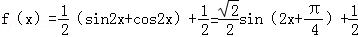
由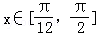
得
，
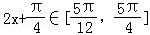所以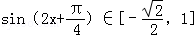
从而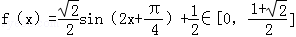
．
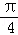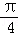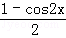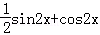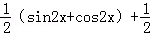
）sin（x﹣）=sin2x+sinxcosx+cos2x=+=∵tanα=2，∴sin2α=2sinαcosα=
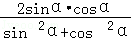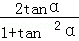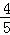==，cos2α=
==
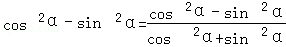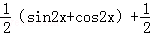
由tanα=2得
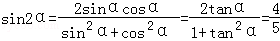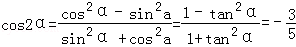，，所以
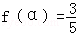．（2）由（1）得
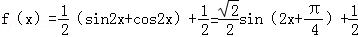
由
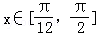得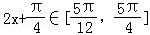，所以
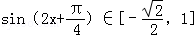
从而
．
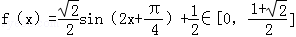练习册系列答案
阅读快车系列答案
相关题目
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2010的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|