题目内容
函数f(x)=
的单调减区间为 .
| (log3x)2-log3x2+x2-6x+10 |
分析:先化简函数,然后求出函数的定义域,根据对数函数的性质以及二次函数的性质,分类讨论每个函数的单调性,从而得到复合函数的单调性.
解答:解:∵f(x)=
,
∴f(x)=
,定义域为(0,+∞),
∵当x∈(0,3]时,log3x≤1,函数(log3x-1)2在(0,3]上单调递减,函数(x-3)2在(0,3]上也单调递减,
∴f(x)=
在(0,3]上单调递减,
∵当x∈(3,+∞)时,log3x>1,函数(log3x-1)2在(3,+∞)上单调递增,函数(x-3)2在(3,+∞)上也单调递增,
∴f(x)=
在(3,+∞)上单调递增,
∴函数f(x)=
的单调减区间为:(0,3].
故答案为:(0,3].
| (log3x)2-log3x2+x2-6x+10 |
∴f(x)=
| (log3x-1)2+(x-3)2 |
∵当x∈(0,3]时,log3x≤1,函数(log3x-1)2在(0,3]上单调递减,函数(x-3)2在(0,3]上也单调递减,
∴f(x)=
| (log3x-1)2+(x-3)2 |
∵当x∈(3,+∞)时,log3x>1,函数(log3x-1)2在(3,+∞)上单调递增,函数(x-3)2在(3,+∞)上也单调递增,
∴f(x)=
| (log3x-1)2+(x-3)2 |
∴函数f(x)=
| (log3x)2-log3x2+x2-6x+10 |
故答案为:(0,3].
点评:本题主要考查了复合函数的单调性,解题的关键弄清每一个函数的单调性,同时考查了分析问题的能力和转化的思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 )2+7lo
)2+7lo +3≤0的解集为M,求当x∈M时,函数f(x)=(lo
+3≤0的解集为M,求当x∈M时,函数f(x)=(lo )(lo
)(lo )的最大值和最小值.
)的最大值和最小值.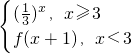 ,则f(2+lo
,则f(2+lo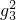 )的值为________.
)的值为________.