题目内容
已知偶函数
在区间
单调递增，则满足
的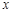
取值范围是( )
A． | B． | C． | D． |
A
解析试题分析：由函数为偶函数，其在区间单调递增，在（
）单调递减，要使，应满足
，或
，所以
所以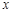取值范围是．
考点：函数的奇偶性和单调性．
练习册系列答案
小学期末标准试卷系列答案
相关题目
命题:“
x∈R,
”的否定是（ ）
A．x∈R, |
B． x∈R, |
| C．x∈R, |
| D．x∈R, |
已知
的反函数图像的对称中心为
，则
的值为（ ）
A． | B．2 | C． | D．3 |
已知函数
为奇函数,且当
时,
则
（ ）
A． | B． | C． | D． |
下列四组函数，两个函数相同的是
A． |
B． |
C． |
D． |
函数
的定义域是 （ ）
A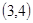． | B． | C． | D． |
函数
的图像关于（ ）
| A．原点对称 | B． 轴对称 | C． 轴对称 | D．直线 对称 |
下列是映射的是（ ）
| A．1、2、3 | B．1、2、5 | C．1、3、5 | D．1、2、3、5 |
设
，若函数
为单调递增函数，且对任意实数，都有
（
是自然对数的底数），则
（ ）
| A．1 | B． | C．3 | D． |