题目内容
已知向量![]() =(sin
=(sin![]() ,cos
,cos![]() ),b=(sin
),b=(sin![]() ,一
,一![]() sin
sin![]() ).
).
(1)求函数![]() 的单调递增区间;
的单调递增区间;
(2)![]() 的图像能否由
的图像能否由![]() 的图像变换得到?若能,请写出变换过程;若不能,请说明理由.
的图像变换得到?若能,请写出变换过程;若不能,请说明理由.
解:(1)![]()
=![]()
=![]()
=![]()
由2k![]() +
+![]() ≤2
≤2![]() +
+![]() ≤2k
≤2k![]() +
+![]() ,得k
,得k![]() +
+![]() ≤
≤![]() ≤k
≤k![]() +
+![]() (k
(k![]() Z)
Z)
∴函数![]() 的单调增区间为[k
的单调增区间为[k![]() +
+![]() ,k
,k![]() +
+![]() ](k
](k![]() Z)
Z)
(2)能由![]() 的图像通过变换得到
的图像通过变换得到![]() 的图像,变换过程如下:
的图像,变换过程如下:
①将![]() 的图像向左平移
的图像向左平移![]() 个单位得到y=sin(
个单位得到y=sin(![]() +
+![]() )的图像;
)的图像;
②再将y=sin(![]() +
+![]() )的图像上各点的纵坐标保持不变,横坐标变为原来的
)的图像上各点的纵坐标保持不变,横坐标变为原来的![]() ,
,
得到y=sin(2![]() +
+![]() )的图像;
)的图像;
③再作y=sin(2![]() +
+![]() )的图像关于
)的图像关于![]() 轴对称的图像,
轴对称的图像,
得到y=-sin(2![]() +
+![]() )的图像;
)的图像;
④最后把y=-sin(2![]() +
+![]() )的图像向上平移
)的图像向上平移![]() 个单位,得
个单位,得![]() 的图像.
的图像.
或者①将![]() 的图像上各点的纵坐标保持不变,横坐标变为原来的
的图像上各点的纵坐标保持不变,横坐标变为原来的![]() ,
,
得到![]() 的图像;
的图像;
②再把![]() 的图像向左平移
的图像向左平移![]() 个单位得到y=sin(2
个单位得到y=sin(2![]() +
+![]() )的图像.
)的图像.
③、④同上.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
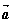 =(sin
=(sin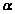 ,2)与向量
,2)与向量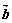 =(cos
=(cos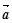 =(sin
=(sin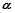 ,2)与向量
,2)与向量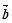 =(cos
=(cos sinωx,cosωx),
sinωx,cosωx), ,记函数f(x)=
,记函数f(x)= ,已知f(x)的周期为π.
,已知f(x)的周期为π.