题目内容
若函数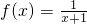
，则函数y=f（f（x））的定义域为________．
{x|x∈R，x≠-1且x≠-2}
分析：根据题意，由分式函数的定义域可得集合A，由解析式的求法可得函数y=f[f（x）]的解析式，进而可得函数y=f（f（x））的定义域．
解答：根据题意，已知函数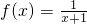，的定义域为A，则A={x|x≠-1}，
y=f[f（x）]=f（
）=
，
令x+2≠0且x≠-1，则函数y=f（f（x））的定义域为B={x|x∈R，x≠-1且x≠-2}；
故答案为：{x|x∈R，x≠-1且x≠-2}．
点评：本题重点考查函数定义域的求法，注意复合函数的定义域的求法．
分析：根据题意，由分式函数的定义域可得集合A，由解析式的求法可得函数y=f[f（x）]的解析式，进而可得函数y=f（f（x））的定义域．
解答：根据题意，已知函数
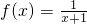，的定义域为A，则A={x|x≠-1}，y=f[f（x）]=f（
）=，令x+2≠0且x≠-1，则函数y=f（f（x））的定义域为B={x|x∈R，x≠-1且x≠-2}；
故答案为：{x|x∈R，x≠-1且x≠-2}．
点评：本题重点考查函数定义域的求法，注意复合函数的定义域的求法．
练习册系列答案
高效智能课时作业系列答案
捷径训练检测卷系列答案
相关题目