题目内容
已知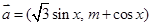 ,
,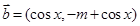 , 且
, 且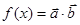
(1) 求函数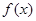 的解析式;
的解析式;
(2) 当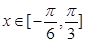 时,
时, 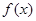 的最小值是-4 , 求此时函数
的最小值是-4 , 求此时函数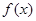 的最大值, 并求出相应的
的最大值, 并求出相应的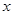 的值.
的值.
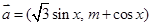 ,
,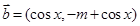 , 且
, 且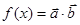
(1) 求函数
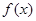 的解析式;
的解析式;(2) 当
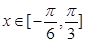 时,
时, 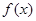 的最小值是-4 , 求此时函数
的最小值是-4 , 求此时函数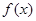 的最大值, 并求出相应的
的最大值, 并求出相应的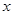 的值.
的值.(1) ;(2)
;(2) 。
。
 ;(2)
;(2) 。
。 试题分析:(1)根据向量数量积的坐标运算可得
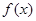 的解析式;(2)由(1)知
的解析式;(2)由(1)知
再由
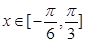 求出
求出 的范围,结合正弦函数的性质可求出
的范围,结合正弦函数的性质可求出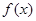 的最大值。
的最大值。 (1)
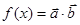

即
 。
。(2)


由
 ,
,  ,
,  ,
, ,
, 
 , 此时
, 此时 , 即
, 即 。
。 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为坐标原点,已知向量
为坐标原点,已知向量 分别对应复数
分别对应复数 ,且
,且 ,
, ,
, 可以与任意实数比较大小,求
可以与任意实数比较大小,求 的值.
的值. 满足
满足 ,则
,则 ( ).
( ).
 ,
, ,且
,且 与夹角为
与夹角为 ,求
,求 ;
;  的夹角
的夹角 ,且
,且 ,则实数
,则实数 =( )
=( )

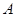 、
、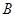 、
、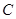 、
、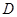 的坐标分别为
的坐标分别为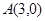 、
、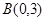 、
、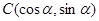 、
、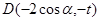 ,
,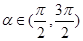
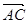 |=|
|=|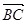 |,求角
|,求角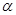 的值;
的值;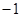 ,求
,求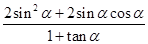 的值.
的值.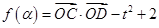 在定义域
在定义域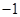 ,求
,求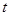 的值.
的值. 的边长为2,则
的边长为2,则 = .
= . _______.
_______.