题目内容
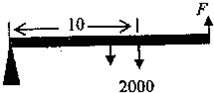如图，重量是2000N的重物挂在杠杆上距支点10米处．质量均匀的杆子每米的重量为100N．（1）杠杆应当为多长，才能使得加在另一端用来平衡重物的力F最小；
（2）若使得加在另一端用来平衡重物的力F最大为2500N，求杠杆长度的变化范围．
分析：（1）设出杠杆的长度为x米，平衡重物的力F做的功等于重物做的功与杠杆自身所做功的和，列式后运用基本不等式求解最小值；
（2）由（1）中得到的力F，由F小于等于2500，整理后得到关于x的一元二次不等式，求解可得范围．
（2）由（1）中得到的力F，由F小于等于2500，整理后得到关于x的一元二次不等式，求解可得范围．
解答：
解：（1）设当杠杆常x米时，在另一端用来平衡重物的力F最小，
则有Fx=10×2000+x×100×
，
F=
+50x≥2
=20000（当且仅当x=20时取“=”）
（2）F=
+50x≤2500，
∴50x2-2500x+20000≤0，
即x-50x+400≤0，解得：10≤x≤40．
解：（1）设当杠杆常x米时，在另一端用来平衡重物的力F最小，则有Fx=10×2000+x×100×
| x |
| 2 |
F=
| 20000 |
| x |
|
（2）F=
| 20000 |
| x |
∴50x2-2500x+20000≤0，
即x-50x+400≤0，解得：10≤x≤40．
点评：本题考查了基本不等式，考查了数学建模思想，训练了运用基本不等式求函数最值，解答此题的关键是正确建立数学模型，是易错题．
练习册系列答案
相关题目
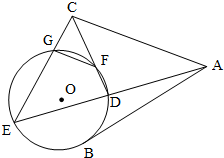如图，AB是⊙O的一条切线，切点为B，ADE，CFD，CGE都是⊙O的割线，已知AC=AB．
A．不等式
选修4-1：几何证明选讲