题目内容
已知数列![]() 的首项
的首项![]() ,前
,前![]() 项和为
项和为![]() ,且
,且![]() .
.
(Ⅰ)证明数列![]() 是等比数列;
是等比数列;
(Ⅱ)令![]() ,求函数
,求函数![]() 在点
在点![]() 处的导数
处的导数![]() ,并比较
,并比较![]() 与
与![]() 的大小.
的大小.
(Ⅰ)证明见答案 (Ⅱ)![]()
解析:
(Ⅰ)由已知![]() ,
,![]() 时,
时,![]() ,
,
两式相减,得![]() ,即
,即![]() ,
,
从而![]() .
.
当![]() 时,
时,![]() ,
,![]() ,
,
又![]() ,
,![]() .从而
.从而![]() .
.
故总有![]() .
.
又![]() ,
,![]() ,从而
,从而![]() ,
,
即![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列.
为公比的等比数列.
(Ⅱ)由(Ⅰ)知![]() .
.
![]() ,
,![]() .
.
从而![]()
![]()
![]()
![]()
![]()
![]() .
.
由上,![]()
![]()
![]() .
. ![]()
当![]() 时,
时,![]() 式
式![]() ,
,![]() ;
;
当![]() 时,
时,![]() 式
式![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,
,
又![]() ,
,
![]() ,即
,即![]()
![]() ,从而
,从而![]() .
.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 的首项
的首项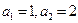 ,前
,前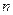 项和
项和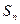 恒为正数,且当
恒为正数,且当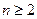 时,
时,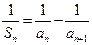 .
.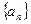 的通项公式;
的通项公式;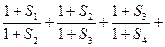
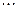
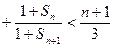 .
.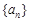 的首项
的首项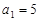 ,前
,前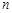 项和为
项和为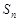 ,且
,且 .
.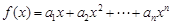 ,求函数
,求函数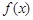 在
在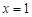 处的导数
处的导数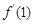 .
.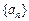 的首项
的首项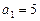 ,前
,前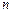 项和为
项和为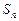 ,且
,且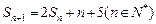 .
.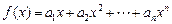 ,求函数
,求函数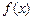 在
在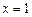 处的导数
处的导数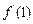 .
.