题目内容
若x≠y,且两个数列x,a1,a2,y和x,b1,b2,b3,y各成等差数列,那么
=( )
| a2-a1 |
| b2-b1 |
分析:设等差数列的公差分别为d1和 d2,则由等差数列的通项公式可得 y=x+3d1=x+4d2,由此求得
=
的值.
| a2-a1 |
| b2-b1 |
| d1 |
| d2 |
解答:解:设等差数列x,a1,a2,y 的公差为d1,等差数列 x,b1,b2,b3,y 的公差为 d2,
则由等差数列的通项公式可得y=x+3d1=x+4d2,
∴
=
=
,
故选D.
则由等差数列的通项公式可得y=x+3d1=x+4d2,
∴
| a2-a1 |
| b2-b1 |
| d1 |
| d2 |
| 4 |
| 3 |
故选D.
点评:本题主要考查等差数列的定义和性质,等差数列的通项公式,求出x+3d1=x+4d2,是解题的关键,属于中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 (2012•卢湾区一模)已知函数f(x)=
(2012•卢湾区一模)已知函数f(x)=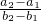 =
=


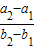 =( )
=( )

