题目内容
函数
的定义域是( )
A．(－ ，－1) | B．(1，＋) |
| C．(－1，1)∪(1，＋) | D．(－，＋) |
C.
解析试题分析：
出现在对数的真数位置，故＞0，即
，又
出现在分式的分母上，故≠0，即
，要使式子有意义，则这两者同时成立，即且，用区间表示即为(－1，1)∪(1，＋).要使式子有意义，则
，解得且，故选C.
考点：函数的定义域求法，对数函数的定义域
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
的图像大致为（ ）
如图甲是某条公共汽车线路收支差额
与乘客量
的图象（收支差额=车票收入-支出费用），由于目前本条线路亏损，公司有关人员提出了两条建议：建议（Ⅰ）是不改变车票价格，减少支出费用；建议（Ⅱ）是不改变支出费用，提高车票价格.下面给出四个图象：在这些图象中( )
| A．①反映了建议（Ⅱ），③反映了建议（Ⅰ） |
| B．①反映了建议（Ⅰ），③反映了建议（Ⅱ） |
| C．②反映了建议（Ⅰ），④反映了建议（Ⅱ） |
| D．④反映了建议（Ⅰ），②反映了建议（Ⅱ） |
函数y=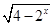
的值域是( )
| A．[0,+∞) | B．[0,2] |
| C．[0,2) | D．(0,2) |
函数f(x)=
则该函数为( )
| A．单调递增函数,奇函数 |
| B．单调递增函数,偶函数 |
| C．单调递减函数,奇函数 |
| D．单调递减函数,偶函数 |
x为实数,[x]表示不超过x的最大整数,则函数f(x)=x-[x]在R上为( )
| A．奇函数 | B．偶函数 |
| C．增函数 | D．周期函数 |
x为实数，[x]表示不超过x的最大整数，则函数f(x)＝x－[x]在R上为( )
| A．奇函数 | B．偶函数 |
| C．增函数 | D．周期函数 |
下列函数中，既是偶函数又在区间(0，＋∞)上单调递减的是( )
A．y＝ | B．y＝e－x |
| C．y＝－x2＋1 | D．y＝lg|x| |
如果f(
)=
,则当x≠0且x≠1时,f(x)=( )
| A． | B． | C． | D．-1 |