题目内容
(本题满分14分)已知函数
 ,
, ,且
,且 为偶函数.设集合
为偶函数.设集合 .
.
(Ⅰ)若 ,记
,记 在
在 上的最大值与最小值分别为
上的最大值与最小值分别为 ,求
,求 ;
;
(Ⅱ)若对任意的实数 ,总存在
,总存在
 ,使得
,使得 对
对 恒成立,试求
恒成立,试求 的最小
的最小
值.
【解析】
试题分析:先利用函数 为偶函数,求出
为偶函数,求出 ,由于二次函数
,由于二次函数 ,在区间
,在区间 上求出最大值
上求出最大值 和最小值
和最小值 ,求出
,求出 ;第二步令
;第二步令 ,由x的范围找出t范围,因
,由x的范围找出t范围,因 ,得
,得 的最大值为
的最大值为 ,从题意分析:在
,从题意分析:在 上,总存在连个点
上,总存在连个点 ,使得
,使得
 成立,只需证明在A上
成立,只需证明在A上 对任意的t成立即可;
对任意的t成立即可;
试题解析:(1)
 为偶函数,所以
为偶函数,所以 .在区间
.在区间 上,
上,

(2)设
 ,
, 所以
所以 的最大值为
的最大值为 ,依题意原命题等价于在
,依题意原命题等价于在 上,总存在两个点
上,总存在两个点 即只需满足在
即只需满足在 上
上  ,因为对任意的
,因为对任意的 都成立,所以当
都成立,所以当 也成立,
也成立,
由(1)知  ,
, ,
,
下面证明在 上总存在两点
上总存在两点 使得
使得 成立.
成立.
当 时,
时, 在
在 上是增函数,
上是增函数,
当 时,
时, 在
在 上是减函数,
上是减函数,
综上所述, 的最小值为
的最小值为 .
.
考点:函数与不等式;

练习册系列答案
相关题目
 ,其中
,其中 ,
, ,定义向量集
,定义向量集 ,若对任意
,若对任意 ,存在
,存在 ,使得
,使得 ,则称
,则称 具有性质
具有性质 .
.  是否具有性质
是否具有性质 ,且
,且 具有性质
具有性质 的值;
的值; ,且当
,且当 时,
时, .
. 到直线
到直线 的距离等于
的距离等于  经过抛物线E:
经过抛物线E: 的焦点,则抛物线E的准线与圆C相交所得弦长为
的焦点,则抛物线E的准线与圆C相交所得弦长为  ,平面
,平面 ,且
,且 ,
, ,则“
,则“ ”是“
”是“ ”的( )
”的( ) 中,底面
中,底面 是平行四边形,点
是平行四边形,点 为
为 的中点,则面
的中点,则面 将四棱锥
将四棱锥
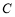 :
: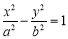
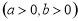 的右顶点为
的右顶点为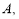
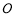 为坐标原点,以
为坐标原点,以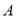 为圆心的圆与双曲线
为圆心的圆与双曲线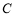 的某渐近线交于两点
的某渐近线交于两点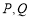 .若
.若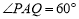 且
且 ,则双曲线
,则双曲线 的离心率为
的离心率为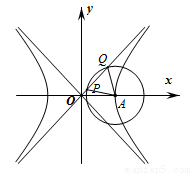
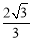 B.
B.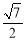 C.
C.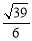 D.
D.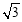
 满足:
满足: ,则
,则 的取值范围是 ,
的取值范围是 , 的最大值为 .
的最大值为 . 则
则 时,
时, 表达式中的展开式中的常数项为 .(用数字作答)
表达式中的展开式中的常数项为 .(用数字作答)