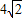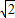题目内容
当x,θ∈R,M=(x+5-3|cosθ|)2+(x-2|sinθ|)2,则M能达到的最小值是
- A.5
- B.

- C.2
- D.

C
分析:通过表达式可知,M是两点的距离的平方,转化为动点到直线y=x的距离的平方的最小值,利用点到直线的距离公式求解即可.
解答:因为要求M=(x+5-3|cosθ|)2+(x-2|sinθ|)2,则M能达到的最小值.
所以M是两点的距离的平方,转化为动点(-5+3|cosθ|,2|sinθ|)到直线y=x的距离的平方的最小值,
即 =
= ,显然当cosθ=1,sinθ=0时,
,显然当cosθ=1,sinθ=0时, 取得最小值为
取得最小值为 .
.
所以M能达到的最小值是2.
故选C.
点评:本题是中档题,考查两点间的距离公式的应用,考查转化思想,计算能力,逻辑推理能力.
分析:通过表达式可知,M是两点的距离的平方,转化为动点到直线y=x的距离的平方的最小值,利用点到直线的距离公式求解即可.
解答:因为要求M=(x+5-3|cosθ|)2+(x-2|sinθ|)2,则M能达到的最小值.
所以M是两点的距离的平方,转化为动点(-5+3|cosθ|,2|sinθ|)到直线y=x的距离的平方的最小值,
即
 =
= ,显然当cosθ=1,sinθ=0时,
,显然当cosθ=1,sinθ=0时, 取得最小值为
取得最小值为 .
.所以M能达到的最小值是2.
故选C.
点评:本题是中档题,考查两点间的距离公式的应用,考查转化思想,计算能力,逻辑推理能力.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目