题目内容
 是定义在
是定义在 上的连续的偶函数,当
上的连续的偶函数,当 时,
时, ,且
,且 ,则不等式
,则不等式 的解集是( )
的解集是( )
A. | B. | C. | D. |
C
解析试题分析:构造函数 、
、 均为偶函数,
均为偶函数, 为偶函数,又
为偶函数,又 时,
时,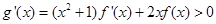 ,
, 在
在 上单调递增,在
上单调递增,在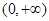 上单调递减,又
上单调递减,又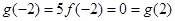 ,
, .
.
考点:1.函数的奇偶性;2.函数的单调性;3.构造函数思想.

练习册系列答案
相关题目
偶函数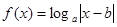 ,在
,在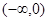 上单调递增,则
上单调递增,则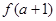 )与
)与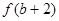 的大小关系是( )
的大小关系是( )
A. | B.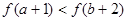 |
C.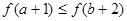 | D.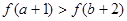 |
函数 的最大值为( )
的最大值为( )
A. | B. | C. | D. |
函数 的值域为( )
的值域为( )
A. | B. | C. | D.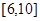 |
已知 在R上是奇函数,且
在R上是奇函数,且
 ( )
( )
A. | B.2 | C. | D.98 |
已知 为
为 上的可导函数,当
上的可导函数,当 时,
时, ,则关于
,则关于 的函数
的函数 的零点个数为( )
的零点个数为( )
| A.1 | B.2 | C.0 | D.0或2 |
 在[-1,2]上的最大值为4,最小值为m,且函数
在[-1,2]上的最大值为4,最小值为m,且函数 在
在 上是增函数,则a=( )
上是增函数,则a=( )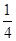

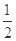

 ,其中
,其中 表示不超过
表示不超过 的最大整数,如
的最大整数,如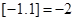 ,
, .若直线
.若直线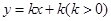 与函数
与函数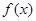 的图象恰好有3个不同的交点,则实数
的图象恰好有3个不同的交点,则实数 的取值范围是 ( )
的取值范围是 ( )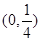
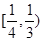


 的⊙
的⊙ 切直线
切直线 于
于 ,射线
,射线 从
从 出发绕着
出发绕着 .旋转过程中,
.旋转过程中, .记
.记 为
为 、弓形
、弓形 的面积为
的面积为 ,那么
,那么 的图象是下面右图中的( )
的图象是下面右图中的( )