题目内容

直线y=x+m与曲线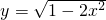 $数学公式$ 有两个交点，则实数m的取值范围是________．

$\text{[math]}$
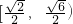
分析：由题意可得曲线 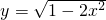$\text{[math]}$ 表示焦点在y轴上的椭圆y²+2x²=1的上半部分联立方程 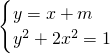$\text{[math]}$ 可得3x²+2mx+m²-1=0，由△=0可得直线与曲线相切时的m，结合图象找出符合条件的m，然后结合图象可知，当直线y=x+m过A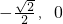（ $\text{[math]}$ ）时，直线y=x+m与椭圆y²+2x²=1的上半部分有2个交点，从而可求
解答：由题意可得曲线 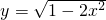$\text{[math]}$ 表示焦点在y轴上的椭圆y²+2x²=1的上半部分
联立方程 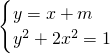$\text{[math]}$ 可得3x²+2mx+m²-1=0
△=4m²-12（m²-1）=0时，m= $\text{[math]}$ 或m= $\text{[math]}$
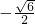
结合图形可知，当m= $\text{[math]}$ 时，直线y=x+m与椭圆y²+2x²=1的上半部分相切
当直线y=x+m过A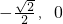（ $\text{[math]}$ ）时，直线y=x+m与椭圆y²+2x²=1的上半部分有2个交点，此时m= $\text{[math]}$
所以， $\text{[math]}$
故答案为： $\text{[math]}$

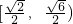
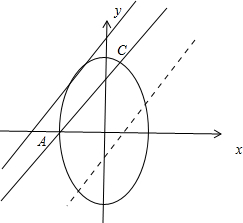
点评：本题主要考查了直线与曲线的位置关系的应用，解题的关键是利用数形结合，要注意此类问题利用结合图象，可以简化基本运算．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

若直线y=x+m与曲线

=x有两个不同的交点，则实数m的取值范围为（　　）

若直线y=x+m与曲线y=

有公共点，则m的取值范围是（　　）

直线y=x+m与曲线x=2

只有一个公共点，则m的范围是

-1≤m≤1，或m=-

-1≤m≤1，或m=-

在直角坐标系xOy中，动点P到两点（0，-

）的距离之和等于4，设动点P的轨迹为曲线C．
（1）写出曲线C的方程；
（2）若直线y=x+m与曲线C有交点，求实数m的取值范围．

直线y=x+m与曲线y=

有两个交点，则实数m的取值范围是