题目内容
已知数列{an}满足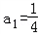 ,
,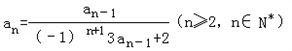 .
.
(1)求数列{an}的通项公式an;
(2)设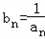 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
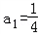 ,
,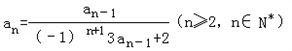 .
.(1)求数列{an}的通项公式an;
(2)设
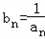 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.解:(1)∵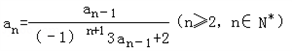 ,
,
∴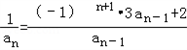 =
=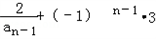 ,
,
∴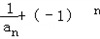 =
=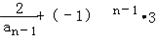 +(﹣1)n
+(﹣1)n
=2[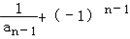 ],
],
∴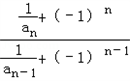 =2,
=2,
∵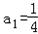 ,∴
,∴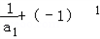 =3,
=3,
∴{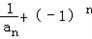 }是以3为首项,以2为公比的等比数列.
}是以3为首项,以2为公比的等比数列.
∴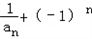 =3×2n﹣1,
=3×2n﹣1,
即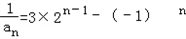 =3×2n﹣1+(-1)n-1,
=3×2n﹣1+(-1)n-1,
∴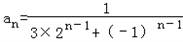 ,
,
(2)∵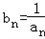 =3×2n﹣1+(﹣1)n﹣1,
=3×2n﹣1+(﹣1)n﹣1,
∴Sn=3×(1+2+22+…+2n﹣1)+[1+(﹣1)+(﹣1)2+…+(﹣1)n﹣1]
=3×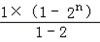 +[1+(﹣1)+(﹣1)2+…+(﹣1)n﹣1]
+[1+(﹣1)+(﹣1)2+…+(﹣1)n﹣1]
=3·2n﹣2+[1+(﹣1)+(﹣1)2+…+(﹣1)n﹣1]
=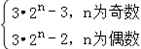 .
.
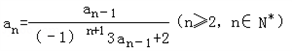 ,
,∴
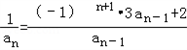 =
=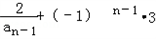 ,
,∴
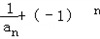 =
=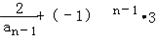 +(﹣1)n
+(﹣1)n=2[
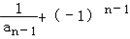 ],
],∴
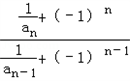 =2,
=2,∵
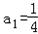 ,∴
,∴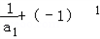 =3,
=3,∴{
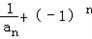 }是以3为首项,以2为公比的等比数列.
}是以3为首项,以2为公比的等比数列.∴
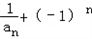 =3×2n﹣1,
=3×2n﹣1,即
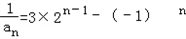 =3×2n﹣1+(-1)n-1,
=3×2n﹣1+(-1)n-1,∴
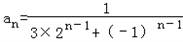 ,
,(2)∵
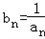 =3×2n﹣1+(﹣1)n﹣1,
=3×2n﹣1+(﹣1)n﹣1,∴Sn=3×(1+2+22+…+2n﹣1)+[1+(﹣1)+(﹣1)2+…+(﹣1)n﹣1]
=3×
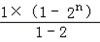 +[1+(﹣1)+(﹣1)2+…+(﹣1)n﹣1]
+[1+(﹣1)+(﹣1)2+…+(﹣1)n﹣1]=3·2n﹣2+[1+(﹣1)+(﹣1)2+…+(﹣1)n﹣1]
=
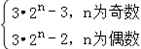 .
.
练习册系列答案
相关题目