题目内容
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
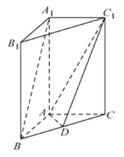
(1)求证:![]() 面
面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1) 略 (2)1/3
【解析】
试题分析:(1)建立空间直角坐标系,求出平面ADC1的法向量,证明![]() =2×2+0×(2)+(4)×1=0,即可证明A1B∥面ADC1;(2)求出:
=2×2+0×(2)+(4)×1=0,即可证明A1B∥面ADC1;(2)求出:![]() =(2,2,0),利用向量的夹角公式,即可求直线
=(2,2,0),利用向量的夹角公式,即可求直线![]() 与平面
与平面![]() 所成角的余弦值
所成角的余弦值
试题解析:(1)证明:如图,以{AB,AC,AA1}为单位正交基底建立空间直角坐标系A-xyz,
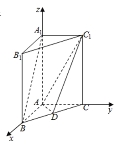
则A(0,0,0),B(2,0,0),C(0,2,0),A1(0,0,4),D(1,1,0),B1(2,0,4),C1(0,2,4)
∴![]() =(2,0,4),
=(2,0,4),![]() =(1,1,0),
=(1,1,0),![]() =(0,2,4),
=(0,2,4),
设平面![]() 的法向量为
的法向量为![]() =(x,y,z),由
=(x,y,z),由![]()
∴![]() 取z=1,得y=-2,x=2,∴平面ADC1的法向量为
取z=1,得y=-2,x=2,∴平面ADC1的法向量为![]() =(2,2,1)
=(2,2,1)
由此可得,![]() =2×2+0×(2)+(4)×1=0,又A1B平面ADC1,∴A1B∥面ADC1.
=2×2+0×(2)+(4)×1=0,又A1B平面ADC1,∴A1B∥面ADC1.
(2)解:![]() =(2,2,0),设直线
=(2,2,0),设直线![]() 与平面
与平面![]() 所成角为θ,则
所成角为θ,则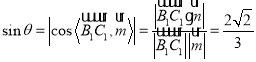 ,
,
又θ为锐角,∴直线![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]()

练习册系列答案
相关题目
【题目】为了对某课题进行研究,用分层抽样方法从三所高校![]() 的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
高校 | 相关人数 | 抽取人数 |
A | 18 |
|
B | 36 | 2 |
C | 54 |
|
(Ⅰ)求![]() ,
,![]() ;
;
(Ⅱ)若从高校![]() 抽取的人中选2人作专题发言,求这二人都来自高校
抽取的人中选2人作专题发言,求这二人都来自高校![]() 的概率.
的概率.