题目内容
已知函数y=x2-4x-5,求:(1)x∈R时的函数值域;
(2)x∈{-1,0,1,2,3,4}时的值域;
(3)x∈[-2,1]时的值域.
思路分析:函数值域是由定义域与对应关系所确定的,在求函数有关问题时,始终要把握好“定义域优先”的原则,二次函数的特定区间求值域值得关注.
解:(1)x∈R,y=x2-4x-5=(x-2)2-9,值域为[-9,+∞).
(2)当x=-1时,y=(-1)2-4×(-1)-5=0;
当x=0时,y=-5;
当x=1时,y=12-4×1-5=-8;
当x=2时,y=22-4×2-5=-9;
当x=3时,y=32-4×3-5=-8;
当x=4时,y=42-4×4-5=-5.
∴当x∈{-1,0,1,2,3,4}时函数y=x2-4x-5的值域为{0,-5,-8,-9}.
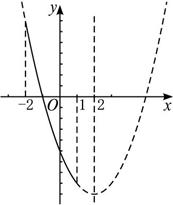
(3)∵y=x2-4x-5的图象如图所示,当x∈[-2,1]时的图象如图所示,由二次函数的性质可知函数y=x2-4x+5在x∈[-2,1]上的最小值为ymin=12-4×1-5=-8,最大值为ymax=(-2)2-4×(-2)-5=7.
∴其值域为[-8,7].

练习册系列答案
相关题目
已知函数y=x2-4|x|+5在(-∞,a)内单调递减,则实数a的取值范围是( )
| A、a≥-2 | B、a≤-2 | C、a≥0 | D、a≤2 |