题目内容
已知
是两个相互垂直的单位向量，
，
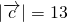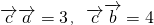，则对于任意t1、t2∈R，当
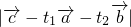取最小值时，函数
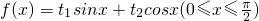的值域是________．
[3，5]
分析：将模平方，利用配方法，可得当且仅当t1=3，t2=4时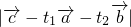，取得最小值，再用辅助角公式，即可求得结论．
解答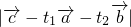：2=
-
+2
∵是两个相互垂直的单位向量，，，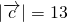
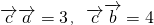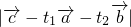∴2=169+t12+t22-6t1-8t2=（t1-3）2+（t2-4）2+144
由此可得，当且仅当t1=3，t2=4时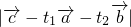，2最小值为144
∴
∴f（x）=5sin（x+α），其中cosα=
，sinα=
∵
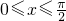，∴3≤5sin（x+α）≤5，
∴函数的值域是[3，5]
故答案为：[3，5]
点评：本题考查向量模的计算，考查配方法的运用，考查三角函数求值，属于中档题．
分析：将模平方，利用配方法，可得当且仅当t1=3，t2=4时，
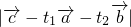取得最小值，再用辅助角公式，即可求得结论．解答：
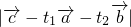2=-+2∵
是两个相互垂直的单位向量，，，∴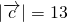
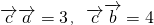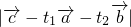2=169+t12+t22-6t1-8t2=（t1-3）2+（t2-4）2+144由此可得，当且仅当t1=3，t2=4时，
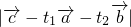2最小值为144∴
∴f（x）=5sin（x+α），其中cosα=
，sinα=∵
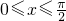，∴3≤5sin（x+α）≤5，∴函数的值域是[3，5]
故答案为：[3，5]
点评：本题考查向量模的计算，考查配方法的运用，考查三角函数求值，属于中档题．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
，
是两个相互垂直的单位向量，而
，
，
。则对于任意实数
，
的最小值是 （ ）
，
是两个相互垂直的单位向量，而
，
，
,则对于任意实数
，
的最小值是( )