题目内容
若向量 ,
, 满足|
满足| |=1,|
|=1,| |=
|= ,且
,且 ⊥(
⊥( +
+ ),则
),则 与
与 的夹角为________.
的夹角为________.
135°(或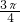 )
)
分析:设 与
与 的夹角为θ,则有
的夹角为θ,则有  =0,化简可得 1=-1×2×cosθ,求出cosθ的值,即可求得
=0,化简可得 1=-1×2×cosθ,求出cosθ的值,即可求得 与
与 的夹角θ的值.
的夹角θ的值.
解答:向量 ,
, 满足|
满足| |=1,|
|=1,| |=
|= ,且
,且 ⊥(
⊥( +
+ ),设
),设 与
与 的夹角为θ,则有
的夹角为θ,则有  =0,即
=0,即  ,故有 1=-1×2×cosθ,
,故有 1=-1×2×cosθ,
∴cosθ=- .
.
再由0≤θ≤π可得 θ= ,
,
故答案为 .
.
点评:本题主要考查两个向量的数量积的定义,两个向量垂直的性质,属于中档题.
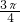 )
)分析:设
 与
与 的夹角为θ,则有
的夹角为θ,则有  =0,化简可得 1=-1×2×cosθ,求出cosθ的值,即可求得
=0,化简可得 1=-1×2×cosθ,求出cosθ的值,即可求得 与
与 的夹角θ的值.
的夹角θ的值.解答:向量
 ,
, 满足|
满足| |=1,|
|=1,| |=
|= ,且
,且 ⊥(
⊥( +
+ ),设
),设 与
与 的夹角为θ,则有
的夹角为θ,则有  =0,即
=0,即  ,故有 1=-1×2×cosθ,
,故有 1=-1×2×cosθ,∴cosθ=-
 .
.再由0≤θ≤π可得 θ=
 ,
,故答案为
 .
.点评:本题主要考查两个向量的数量积的定义,两个向量垂直的性质,属于中档题.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
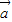 ,
,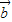 满足|
满足|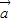 |=1,|
|=1,|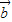 |=2,且
|=2,且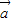 ,
,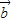 的夹角为
的夹角为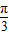 ,则
,则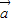 •
• = ,|
= ,| +
+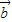 |= .
|= . ,
, 满足|
满足|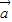 |=|
|=|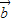 |=1,且
|=1,且 •
•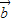 +
+ •
•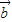 =
= ,则向量
,则向量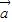 ,
,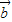 的夹角为( )
的夹角为( ) ,
, 满足|
满足| |=1,|
|=1,| |=
|= ,且
,且 ⊥
⊥ ,则
,则 与
与 的夹角为( )
的夹角为( )



 ,
, 满足|
满足| |=|
|=| |=|
|=| +
+ |=1,则
|=1,则 •
• 的值为 .
的值为 .