Question

已知双曲线-=1(a＞0,b＞0)的左、右顶点分别为A、B，右焦点为F(c,0)(c＞0)，右准线为l:x=,|AF|=3.过点F作直线交双曲线的右支于P、Q两点，延长PB交右准线l于M点.

(1)求双曲线的方程；

(2)若·=-17，求△PBQ的面积S.

Answer 1

解：(1)由题意知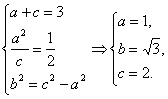

    则双曲线方程为x²-=1.

    (2)设P(x₁,y₁)、Q(x₂,y₂)，易得F(2,0)、A(-1,0)、B(1,0)，右准线l:x=,设PQ方程为y=k(x-2),

    代入双曲线方程可得(3-k²)x²+4k²x-(4k²+3)=0.

    由于P、Q都在双曲线的右支上，所以

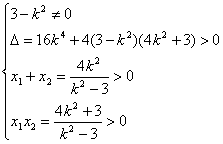
    k²＞3.

    ∴y₁y₂=k(x₁-2)·k(x₂-2)=k²［x₁x₂-2(x₁+x₂)+4］=.

    由于=(x₁,y₁), =(x₂,y₂),

    由·=-17,可得x₁x₂+y₁y₂=-17-=-17k²=4.

    此时x₁+x₂=16,x₁x₂=19,y₁y₂=-36.

    ∴y₁+y₂=k(x₁-2)+k(x₂-2)

    =k(x₁+x₂-4)

    =12k.

    ∴S_△PBQ=|BF|×|y₁-y₂|

    =×1×

    =

    =

    =65.