题目内容
已知向量a=(1,2),b=(cosα,sinα),设m=a+tb(t为实数)。
(1)若 ,求当|m|取最小值时实数t的值;
,求当|m|取最小值时实数t的值;
(2)若a⊥b,问:是否存在实数t,使得向量a-b和向量m的夹角为 ,若存在,请求出t的值;若不存在,请说明理由。
,若存在,请求出t的值;若不存在,请说明理由。
(1)若
 ,求当|m|取最小值时实数t的值;
,求当|m|取最小值时实数t的值;(2)若a⊥b,问:是否存在实数t,使得向量a-b和向量m的夹角为
 ,若存在,请求出t的值;若不存在,请说明理由。
,若存在,请求出t的值;若不存在,请说明理由。解:(1)因为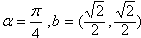 ,a·b=
,a·b=
则

所以当 时,|m|取最小值,最小值为
时,|m|取最小值,最小值为 。
。
(2)由条件得
又因为|a-b|= ,
,
 ·
·
则有
且t<5,整理得t2+5t-5=0,
所以存在 满足条件。
满足条件。
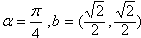 ,a·b=
,a·b=
则


所以当
 时,|m|取最小值,最小值为
时,|m|取最小值,最小值为 。
。(2)由条件得

又因为|a-b|=
 ,
,
 ·
·
则有

且t<5,整理得t2+5t-5=0,
所以存在
 满足条件。
满足条件。
练习册系列答案
相关题目