题目内容
已知数列{an}满足a1=4,an=4-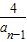 (n≥2,n∈N*),令
(n≥2,n∈N*),令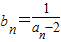
(1)求数列{bn}的通项公式;
(2)当n∈N*时,求证:
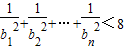 .
.
【答案】分析:(1)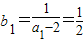 ,由
,由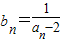 知
知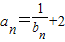 .代入已知得
.代入已知得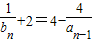 转化为
转化为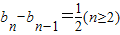 ,利用等差数列的通项公式即可得出.
,利用等差数列的通项公式即可得出.
(2)当n≥2时,通过放缩和裂项可得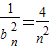
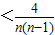 =
=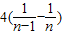 .进而即可证明.
.进而即可证明.
解答:解:(1)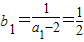 ,由
,由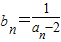 知
知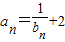 .
.
代入已知得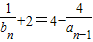 即
即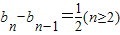 .
.
故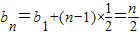 .
.
(2)当n≥2时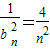
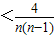 =
=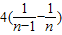 .
.
当n=1时,不等式成立
当n≥2时,左边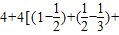 …+
…+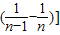 =
=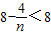 .
.
点评:正确变形、利用等差数列的通项公式和放缩法、裂项求和即可得出.
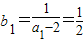 ,由
,由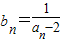 知
知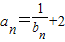 .代入已知得
.代入已知得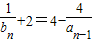 转化为
转化为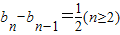 ,利用等差数列的通项公式即可得出.
,利用等差数列的通项公式即可得出.(2)当n≥2时,通过放缩和裂项可得
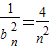
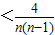 =
=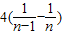 .进而即可证明.
.进而即可证明.解答:解:(1)
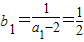 ,由
,由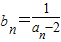 知
知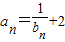 .
.代入已知得
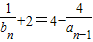 即
即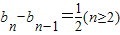 .
.故
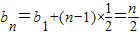 .
.(2)当n≥2时
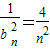
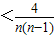 =
=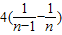 .
.当n=1时,不等式成立
当n≥2时,左边
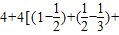 …+
…+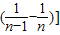 =
=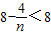 .
.点评:正确变形、利用等差数列的通项公式和放缩法、裂项求和即可得出.

练习册系列答案
相关题目