题目内容
已知集合A{x|y=
},集合B={x|y=ln(4-3x-x2)},集合C={x|m+2<x<2m-3}.
(Ⅰ)设全集U=R,求?UA∩B;
(Ⅱ)若A∩C=C,求实数m的取值范围.
| x2-7x-18 |
(Ⅰ)设全集U=R,求?UA∩B;
(Ⅱ)若A∩C=C,求实数m的取值范围.
分析:(Ⅰ)通过求函数的定义域化简集合A与B,然后利用补集和交集的概念求解;
(Ⅱ)由A∩C=C,∴C⊆A,然后利用两集合端点值间的关系列式求解m的范围.
(Ⅱ)由A∩C=C,∴C⊆A,然后利用两集合端点值间的关系列式求解m的范围.
解答:解:(Ⅰ)由A={x|y=
}=(-∞,2]∪[9,+∞),
B={x|y=ln(4-3x-x2)}=(-4,1),
所以?UA=(-2,9),?UA∩B=(-2,1);
(Ⅱ)∵A∩C=C,∴C⊆A,
当C=∅时,m+2≥2m-3,解得m≤5,
当C≠∅时,
或
,解得:m≥7,
综上:实数m的取值范围是{m|m≤5或m≥7}.
| x2-7x-18 |
B={x|y=ln(4-3x-x2)}=(-4,1),
所以?UA=(-2,9),?UA∩B=(-2,1);
(Ⅱ)∵A∩C=C,∴C⊆A,
当C=∅时,m+2≥2m-3,解得m≤5,
当C≠∅时,
|
|
综上:实数m的取值范围是{m|m≤5或m≥7}.
点评:本题考查了交、并、补集的混合运算,考查了函数的定义域的求法,解答的关键是对区间端点值的取舍,是基础题.

练习册系列答案
相关题目
已知集合A={x|y=
,x∈Z},B={y|y=x2+1,x∈A},则A∩B为( )
| 1-x2 |
| A、∅ | B、{1} |
| C、[0,+∞) | D、{(0,1)} |
已知集合A={x|y=
},B={y|y=3x,x>0},定义A*B为图中阴影部分的集合,则A*B( )
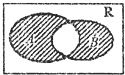
| 2x-x2 |

| A、{x|0<x<2} |
| B、{x|1<x≤2} |
| C、{x|0≤x≤1或x≥2} |
| D、{x|0≤x≤1或x>2} |
已知集合A={x|y=lg(x+3)},B={x|x≥2},则下列结论正确的是( )
| A、-3∈A | B、3∉B | C、A∪B=B | D、A∩B=B |
已知集合A={x|y=lgx},B={x|x2+x-2≤0},则A∩B=( )
| A、[-1,0) | B、(0,1] | C、[0,1] | D、[-2,1] |