题目内容
下列说法正确的是
- A.定义在R上的函数f(x)满足f(2)>f(1),则f(x)在R上是增函数
- B.定义在R上的函数f(x)满足f(2)>f(1),则f(x)在R上不是减函数
- C.y=tanx在定义域上是增函数
- D.若f(x+1)是奇函数,则f(-x-1)=-f(x+1)
B
分析:定义在R上的函数f(x)满足f(2)>f(1),则f(x)在R上不一定是增函数;
定义在R上的函数f(x)满足f(2)>f(1),则f(x)在R上不是减函数;
y=tanx的增区间是(- ,
, );
);
若f(x+1)是奇函数,则f(-x+1)=-f(x+1).
解答:定义在R上的函数f(x)满足f(2)>f(1),
则f(x)在R上不一定是增函数,故A不正确;
定义在R上的函数f(x)满足f(2)>f(1),
则f(x)在R上不是减函数,故B正确;
y=tanx的增区间是(- ,
, ),故C不正确;
),故C不正确;
若f(x+1)是奇函数,则f(-x+1)=-f(x+1),故D不正确.
故选B.
点评:本题考查复合命题的真假判断,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.
分析:定义在R上的函数f(x)满足f(2)>f(1),则f(x)在R上不一定是增函数;
定义在R上的函数f(x)满足f(2)>f(1),则f(x)在R上不是减函数;
y=tanx的增区间是(-
 ,
, );
);若f(x+1)是奇函数,则f(-x+1)=-f(x+1).
解答:定义在R上的函数f(x)满足f(2)>f(1),
则f(x)在R上不一定是增函数,故A不正确;
定义在R上的函数f(x)满足f(2)>f(1),
则f(x)在R上不是减函数,故B正确;
y=tanx的增区间是(-
 ,
, ),故C不正确;
),故C不正确;若f(x+1)是奇函数,则f(-x+1)=-f(x+1),故D不正确.
故选B.
点评:本题考查复合命题的真假判断,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
 ,则下列说法正确的是( )
,则下列说法正确的是( ) 有且只有一个零点
B.
有且只有一个零点
B. ,
, ,则下列说法正确的是( )
,则下列说法正确的是( )
 ,乙比甲成绩稳定,应该选乙参加比赛
,乙比甲成绩稳定,应该选乙参加比赛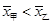 ,甲比乙成绩稳定,应该选甲参加比赛
,甲比乙成绩稳定,应该选甲参加比赛 :函数
:函数 (
( 且
且 )的图像恒过点
)的图像恒过点 ;
; :函数
:函数 有两个零点.
有两个零点.  为假命题 D.
为假命题 D. 为真命题
为真命题 的导函数
的导函数 的图象如上图所示,则下列说法正确的是 ( )
的图象如上图所示,则下列说法正确的是 ( ) 内单调递减 B、函数
内单调递减 B、函数 内单调递增
内单调递增 处取极大值 D、函数
处取极大值 D、函数 处取极小值
处取极小值