题目内容
已知函数f(x)=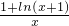
(1)求函数的定义域;
(2)确定函数f(x)在定义域上的单调性,并证明你的结论;
(3)当x>0时,f(x)>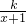 恒成立,求正整数k的最大值.
恒成立,求正整数k的最大值.
解:(1)根据函数f(x)=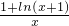 ,可得 x≠0,且 x+1>0,由此求得函数的定义域为 {x|x>-1,且 x≠0}.
,可得 x≠0,且 x+1>0,由此求得函数的定义域为 {x|x>-1,且 x≠0}.
(2)f′(x)= [
[ -1-ln(x+1)]=-
-1-ln(x+1)]=- [-
[- +ln(x+1)+1].
+ln(x+1)+1].
当 x>0 时,1> >0,ln(x+1)>0,
>0,ln(x+1)>0, >0,∴f′(x)=-
>0,∴f′(x)=- [-
[- +ln(x+1)+1]<0,故函数f(x)在(0,+∞)上是减函数.
+ln(x+1)+1]<0,故函数f(x)在(0,+∞)上是减函数.
当 0>x>-1 时,令g(x)=[ +ln(x+1)+1],g′(x)=-
+ln(x+1)+1],g′(x)=-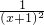 +
+ =
= <0,
<0,
故g(x)在(-1,0)上是减函数,故g(x)>g(0)=1>0,故 f′(x)=- [
[ +ln(x+1)+1]<0,故函数f(x)在(-1,0)上是减函数.
+ln(x+1)+1]<0,故函数f(x)在(-1,0)上是减函数.
综上可得,函数f(x)在(0,+∞)、(-1,0)上是减函数.
(3)当x>0时,f(x)>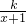 恒成立,令x=1可得,k<2(1+ln2),再由k 为正整数,故k的最大值不大于3.
恒成立,令x=1可得,k<2(1+ln2),再由k 为正整数,故k的最大值不大于3.
下面证明k=3 时,f(x)>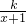 (x>0)恒成立,即证当x>0时,(x+1)ln(x+1)+1-2x>0恒成立.
(x>0)恒成立,即证当x>0时,(x+1)ln(x+1)+1-2x>0恒成立.
令h(x)=(x+1)ln(x+1)+1-2x,则 h′(x)=ln(x+1)-1.
当 x>e-1时,h′(x)>0,当 0<x<e-1时,h′(x)<0,故当 x=e-1时,h(x)取得最小值为 h(e-1)=3-e>0.
故当x>0时,(x+1)ln(x+1)+1-2x>0恒成立,故k的最大值为3.
分析:(1)根据函数的解析式可得 x≠0,且 x+1>0,由此求得函数的定义域.
(2)求出f′(x),分x>0 以及0>x>-1两种情况,都可得到函数f′(x)<0,从而得到函数f(x)在(0,+∞)、(-1,0)上是减函数.
(3)当x>0时,f(x)>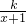 恒成立,令x=1可得,k<2(1+ln2),再由k 为正整数,故k的最大值不大于3.k=3 时,即证当x>0时,(x+1)ln(x+1)+1-2x>0恒成立.
恒成立,令x=1可得,k<2(1+ln2),再由k 为正整数,故k的最大值不大于3.k=3 时,即证当x>0时,(x+1)ln(x+1)+1-2x>0恒成立.
利用导数求出h(x)=(x+1)ln(x+1)+1-2x 的最小值等于3-e>0,从而得到正整数k的最大值.
点评:本题主要考查利用导数研究函数的单调性,对数函数的图象和性质的应用,属于中档题.
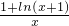 ,可得 x≠0,且 x+1>0,由此求得函数的定义域为 {x|x>-1,且 x≠0}.
,可得 x≠0,且 x+1>0,由此求得函数的定义域为 {x|x>-1,且 x≠0}.(2)f′(x)=
 [
[ -1-ln(x+1)]=-
-1-ln(x+1)]=- [-
[- +ln(x+1)+1].
+ln(x+1)+1]. 当 x>0 时,1>
 >0,ln(x+1)>0,
>0,ln(x+1)>0, >0,∴f′(x)=-
>0,∴f′(x)=- [-
[- +ln(x+1)+1]<0,故函数f(x)在(0,+∞)上是减函数.
+ln(x+1)+1]<0,故函数f(x)在(0,+∞)上是减函数.当 0>x>-1 时,令g(x)=[
 +ln(x+1)+1],g′(x)=-
+ln(x+1)+1],g′(x)=-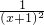 +
+ =
= <0,
<0,故g(x)在(-1,0)上是减函数,故g(x)>g(0)=1>0,故 f′(x)=-
 [
[ +ln(x+1)+1]<0,故函数f(x)在(-1,0)上是减函数.
+ln(x+1)+1]<0,故函数f(x)在(-1,0)上是减函数.综上可得,函数f(x)在(0,+∞)、(-1,0)上是减函数.
(3)当x>0时,f(x)>
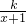 恒成立,令x=1可得,k<2(1+ln2),再由k 为正整数,故k的最大值不大于3.
恒成立,令x=1可得,k<2(1+ln2),再由k 为正整数,故k的最大值不大于3.下面证明k=3 时,f(x)>
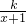 (x>0)恒成立,即证当x>0时,(x+1)ln(x+1)+1-2x>0恒成立.
(x>0)恒成立,即证当x>0时,(x+1)ln(x+1)+1-2x>0恒成立.令h(x)=(x+1)ln(x+1)+1-2x,则 h′(x)=ln(x+1)-1.
当 x>e-1时,h′(x)>0,当 0<x<e-1时,h′(x)<0,故当 x=e-1时,h(x)取得最小值为 h(e-1)=3-e>0.
故当x>0时,(x+1)ln(x+1)+1-2x>0恒成立,故k的最大值为3.
分析:(1)根据函数的解析式可得 x≠0,且 x+1>0,由此求得函数的定义域.
(2)求出f′(x),分x>0 以及0>x>-1两种情况,都可得到函数f′(x)<0,从而得到函数f(x)在(0,+∞)、(-1,0)上是减函数.
(3)当x>0时,f(x)>
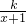 恒成立,令x=1可得,k<2(1+ln2),再由k 为正整数,故k的最大值不大于3.k=3 时,即证当x>0时,(x+1)ln(x+1)+1-2x>0恒成立.
恒成立,令x=1可得,k<2(1+ln2),再由k 为正整数,故k的最大值不大于3.k=3 时,即证当x>0时,(x+1)ln(x+1)+1-2x>0恒成立.利用导数求出h(x)=(x+1)ln(x+1)+1-2x 的最小值等于3-e>0,从而得到正整数k的最大值.
点评:本题主要考查利用导数研究函数的单调性,对数函数的图象和性质的应用,属于中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|