题目内容
【题目】在平面直角坐标系中,已知点![]() ,
,![]() ,动点
,动点![]() 满足直线
满足直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() .记点
.记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的方程,并说明
的方程,并说明![]() 是什么曲线;
是什么曲线;
(2)若![]() ,
,![]() 是曲线
是曲线![]() 上的动点,且直线
上的动点,且直线![]() 过点
过点![]() ,问在
,问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() ?若存在,请求出定点
?若存在,请求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ,椭圆;(2)存在,
,椭圆;(2)存在,![]() .
.
【解析】
(1)写出斜率,根据斜率之积为![]() 建立方程,化简即可(2)假设存在的定点
建立方程,化简即可(2)假设存在的定点![]() ,分MN斜率存在或不存在两种情况讨论,设
,分MN斜率存在或不存在两种情况讨论,设![]() ,
,![]() ,当MN斜率存在时,联立方程可求出
,当MN斜率存在时,联立方程可求出![]() ,根据两角相等可得
,根据两角相等可得![]() ,化简即可求出m,验证MN斜率不存在时也成立即可.
,化简即可求出m,验证MN斜率不存在时也成立即可.
(1)由题意得:![]()
![]()
化简得:![]()
![]() 曲线
曲线![]() 的方程为
的方程为![]()
![]() 是中心在坐标原点,焦点在
是中心在坐标原点,焦点在![]() 轴上的椭圆(不含左、右顶点)
轴上的椭圆(不含左、右顶点)
(2)假设存在的定点![]() 符合题意
符合题意
由题意知:直线![]() 的斜率分别为
的斜率分别为![]() ,
,![]()
由题意及(1)知:直线![]() 与直线
与直线![]() 均不重合.
均不重合.
当直线![]() 的斜率
的斜率![]() 存在时
存在时
设其方程为![]() ,
,![]() ,
,![]()
由![]() ,得直线
,得直线![]() 的倾斜角互补,故
的倾斜角互补,故![]()
又![]()
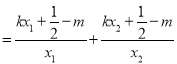
![]()
![]() ①
①
由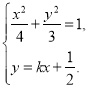 消去
消去![]() ,整理得:
,整理得:![]() .
.
![]()
又![]() ,
,![]() ②
②
代②入①得:![]()
![]() ③
③
![]() 当
当![]() 时,又
时,又![]() 不恒为0
不恒为0
![]() 当且仅当
当且仅当![]() 时,③式成立,即定点
时,③式成立,即定点![]() 满足题意.
满足题意.
当直线![]() 的斜率不存在时,点
的斜率不存在时,点![]() 满足
满足![]() ,也符合题意.
,也符合题意.
综上所述,在 ![]() 轴上存在定点
轴上存在定点![]() ,使得
,使得![]() .
.

练习册系列答案
相关题目
【题目】在![]() 年俄罗斯索契冬奥会某项目的选拔比赛中,
年俄罗斯索契冬奥会某项目的选拔比赛中,![]() 、
、![]() 两个代表队进行对抗赛,每队三名队员,
两个代表队进行对抗赛,每队三名队员,![]() 队队员是
队队员是![]() 、
、![]() 、
、![]() ,
,![]() 队队员是
队队员是![]() 、
、![]() 、
、![]() ,按以往多次比赛的统计,对阵队员之间胜负概率如下表,现按表中对阵方式出场进行三场比赛,每场胜队得
,按以往多次比赛的统计,对阵队员之间胜负概率如下表,现按表中对阵方式出场进行三场比赛,每场胜队得![]() 分,负队得
分,负队得![]() 分,设
分,设![]() 队、
队、![]() 队最后所得总分分别为
队最后所得总分分别为![]() 、
、![]() 且
且![]() .
.
对阵队员 |
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 队得分为
队得分为![]() 分的概率;
分的概率;
(2)求![]() 的分布列;并用统计学的知识说明哪个队实力较强.
的分布列;并用统计学的知识说明哪个队实力较强.