题目内容
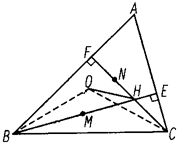
（2008•南京模拟）选修4-1：几何证明选讲如图，在△ABC中，∠A=60°，AB＞AC，点O是外心，两条高 BE，CF交于H点，点M，N分别在线段BH，FH上，且满足BM=CN，求
| MH+NH | OH |
分析：在BE上取BK=CH，连接OB、OC、OK，由圆周角定理及∠A=60°可得∠BOC=120°，而由重心的性质，可得∠BHC=120°，进而根据四点共圆的判定方法，得到B、C、H、O四点共圆，进而可得△BOK≌△COH，根据正弦定理，我们可得KH=
OH，进而根据MH+NH=MH+KM=KH，即可得到答案．
| 3 |
解答：解：如图在BE上取BK=CH，连接OB、OC、OK，
由三角形的外心的性质可知：∠BOC=2∠A=120°，
由三角形的垂心性质可知：∠BHC=180°-∠A=120°，
所以∠BOC=∠BHC，所以B、C、H、O四点共圆，∠OBH=∠OCH，…（3分）
又因为OB=OC，BK=CH，所以△BOK≌△COH，
因为∠BOK=∠COH，OK=OH，所以∠KOH=∠BOC=120°，∠OKH=∠OHK=30°，…（6分）
观察△OKH，有：
=
，则KH=
OH，
又因为BM=CN，BK=CH，所以KM=NH，所以MH+NH=MH+KM=KH=
OH，
故
=
．…（8分）
由三角形的外心的性质可知：∠BOC=2∠A=120°，
由三角形的垂心性质可知：∠BHC=180°-∠A=120°，
所以∠BOC=∠BHC，所以B、C、H、O四点共圆，∠OBH=∠OCH，…（3分）
又因为OB=OC，BK=CH，所以△BOK≌△COH，
因为∠BOK=∠COH，OK=OH，所以∠KOH=∠BOC=120°，∠OKH=∠OHK=30°，…（6分）
观察△OKH，有：
| KH |
| sin120° |
| OH |
| sin30° |
| 3 |
又因为BM=CN，BK=CH，所以KM=NH，所以MH+NH=MH+KM=KH=
| 3 |
故
| MH+NH |
| OH |
| 3 |
点评：本题考查的知识点是三角形的外心，三角形的垂心，圆内接四边形（四点共圆）的判定与性质，圆周角定理，三角形全等的判定和性质，其中添加恰当的辅助线构造出全等的三角形，是解答本题的关键．本题辅助线添加方法比较困难，解答过程涉及知识点比较多，是平面几何中的难题．
练习册系列答案
相关题目
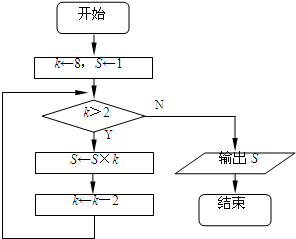（2008•南京模拟）如图所示的流程图输出的结果是