题目内容
在四边形ABCD中，|| AD |
| CD |
| AB |
| DA |
| DC |
| AC |
| AB |
| AC |
分析：设∠BAC=α，∠DAC=β．由于|
+
|=|
|，可得|
+
|=|
-
|，于是∠ADC=90°，利用直角三角形的边角关系和平方关系可得sinβ，cosβ，利用投影可得cosα，进而得到sinα，再利用两角和差的正弦公式即可得出．
| DA |
| DC |
| AC |
| DA |
| DC |
| DC |
| DA |
解答：解：如图所示，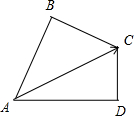
设∠BAC=α，∠DAC=β．
∵|
+
|=|
|，
∴|
+
|=|
-
|，
∴∠ADC=90°．
∴|
|=
=
=13．
∴cosβ=
，sinβ=
．
∵
在
方向上的投影为8，∴|
|cosα=8，解得cosα=
=
．
∴sinα=
=
．
∴sin∠BAD=sin（α+β）=sinαcosβ+cosαsinβ
=
×
+
×
=
．
故答案为：
．
设∠BAC=α，∠DAC=β．
∵|
| DA |
| DC |
| AC |
∴|
| DA |
| DC |
| DC |
| DA |
∴∠ADC=90°．
∴|
| AC |
|
|
| 122+52 |
∴cosβ=
| 12 |
| 13 |
| 5 |
| 13 |
∵
| AB |
| AC |
| AB |
| 8 |
| 10 |
| 4 |
| 5 |
∴sinα=
| 1-cos2α |
| 3 |
| 5 |
∴sin∠BAD=sin（α+β）=sinαcosβ+cosαsinβ
=
| 3 |
| 5 |
| 12 |
| 13 |
| 4 |
| 5 |
| 5 |
| 13 |
| 56 |
| 65 |
故答案为：
| 56 |
| 65 |
点评：本题综合考查了向量的运算法则、数量积运算的性质、三角函数的基本关系式、两角和差的正弦公式等基础知识与基本技能方法，属于中档题．
练习册系列答案
相关题目
如图所示，在四边形ABCD中，EF∥BC，FG∥AD，则