题目内容
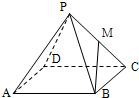
 已知正四棱锥P-ABCD中,底面是边长为2的正方形,高为
已知正四棱锥P-ABCD中,底面是边长为2的正方形,高为| 2 |
(Ⅰ) 求证:PA∥平面MDB;
(Ⅱ) N为AP的中点,求CN与平面MBD所成角的正切值.
分析:(1)连接MO,可得MO是△PAC的中位线,再根据线面平行的判定定理可得结论.
(2)令NC∩MO=Q,先证明PC⊥平面BMD,再根据三角形的中位线定理求出MQ的长,可得∠MQC是直线NC与平面BMD所成的角,在Rt△CMQ中求出即可.
(2)令NC∩MO=Q,先证明PC⊥平面BMD,再根据三角形的中位线定理求出MQ的长,可得∠MQC是直线NC与平面BMD所成的角,在Rt△CMQ中求出即可.
解答:证明:(1)如图所示,连接AC交BD于O,连接MO.
在△PAC中,OM为中位线,∴OM∥PA.
∴
∴PA∥平面MDB.
(2)令NC∩MO=Q.连接PO.
∵此四棱锥P-ABCD是正四棱锥,∴PO⊥底面ABCD.
在Rt△AOP中,PA=
=2.
同理PA=PB=PC=PD=AB=BC=CD=DA=2.
∵M是PC中点,∴在△PDC中,DM⊥PC.
同理,在△PBC中,BM⊥PC.
在平面BMD中,BM∩DM=M.
∴PC⊥平面MDB.
∴∠CQM为CN与平面MBD所成角的平面角.
∵M是线段PC的中点,∴MC=1.
由(1)可知:PA∥平面BMD,平面PAC∩平面BMD=OM.
∴PA∥MO,
又∵PM=MC,∴OM是△PAC的中位线,∴MQ=
PN=
.
在Rt△CMQ中,tan∠CQM=
=2.
CN与平面MBD所成角的正切值是2.

在△PAC中,OM为中位线,∴OM∥PA.
∴
|
∴PA∥平面MDB.
(2)令NC∩MO=Q.连接PO.
∵此四棱锥P-ABCD是正四棱锥,∴PO⊥底面ABCD.
在Rt△AOP中,PA=
(
|
同理PA=PB=PC=PD=AB=BC=CD=DA=2.
∵M是PC中点,∴在△PDC中,DM⊥PC.
同理,在△PBC中,BM⊥PC.
在平面BMD中,BM∩DM=M.
∴PC⊥平面MDB.
∴∠CQM为CN与平面MBD所成角的平面角.
∵M是线段PC的中点,∴MC=1.
由(1)可知:PA∥平面BMD,平面PAC∩平面BMD=OM.
∴PA∥MO,
又∵PM=MC,∴OM是△PAC的中位线,∴MQ=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△CMQ中,tan∠CQM=
| MC |
| MQ |
CN与平面MBD所成角的正切值是2.
点评:掌握线面平行、垂直的判定定理和性质定理、线面角是解题的关键.利用三角形的中位线定理是证明线线平行常用的方法之一.

练习册系列答案
相关题目
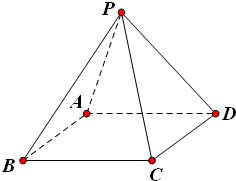 已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.
已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.
 已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h.
已知正四棱锥P-ABCD的全面积为2,记正四棱锥的高为h. ,M是侧棱PC的中点,则异面直线PA与BM所成角为 .
,M是侧棱PC的中点,则异面直线PA与BM所成角为 .