题目内容
(2014•广东模拟)在极坐标系中,圆C1的方程为ρ=4
cos(θ-
),以极点为坐标原点,极轴为x轴的正半轴建立平面坐标系,圆C2的参数方程
(θ为参数),若圆C1与C2相切,则实数a=
| 2 |
| π |
| 4 |
|
±
或±5
| 2 |
| 2 |
±
或±5
.| 2 |
| 2 |
分析:先根据ρ2=x2+y2,x=ρcos θ,y=ρsin θ,将圆C1的方程化成直角坐标方程,再利用同角三角函数关系消去θ,可得圆C2的直角坐标方程,最后根据圆C1与圆C2相切,分为外切的内切两种情况讨论,利用圆心距与半径之间的关系建立方程,求实数a的值.
解答:解:∵圆C1的方程为ρ=4
cos(θ-
),
∴⊙C1的方程化为ρ=4cos θ+4sin θ,则ρ2=4ρcos θ+4ρsin θ,
由ρ2=x2+y2,x=ρcos θ,y=ρsin θ,得x2+y2-4x-4y=0,
∴圆心C1坐标为(2,2),半径r1=2
,
∵圆C2的参数方程是
,
∴其普通方程是(x+1)2+(y+1)2=a2,
∴以C2的坐标是(-1,-1),r2=|a|,
∵两圆相切,
∴当外切时|C1C2|=|a|+2
=
=3
,解得a=±
,
内切时|C1C2|=|a|-2
=
=3
,解得a=±5
∴a=±
或±5
.
故答案为:±
或±5
.
| 2 |
| π |
| 4 |
∴⊙C1的方程化为ρ=4cos θ+4sin θ,则ρ2=4ρcos θ+4ρsin θ,
由ρ2=x2+y2,x=ρcos θ,y=ρsin θ,得x2+y2-4x-4y=0,
∴圆心C1坐标为(2,2),半径r1=2
| 2 |
∵圆C2的参数方程是
|
∴其普通方程是(x+1)2+(y+1)2=a2,
∴以C2的坐标是(-1,-1),r2=|a|,
∵两圆相切,
∴当外切时|C1C2|=|a|+2
| 2 |
| (2+1)2+(2+1)2 |
| 2 |
| 2 |
内切时|C1C2|=|a|-2
| 2 |
| (2+1)2+(2+1)2 |
| 2 |
| 2 |
∴a=±
| 2 |
| 2 |
故答案为:±
| 2 |
| 2 |
点评:本题考查参数方程化成普通方程、简单曲线的极坐标方程、圆与圆的位置关系及其应用.解题时要认真审题,把极坐标方程合理地转化为普通方程.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
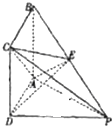 (2014•广东模拟)如图,四棱锥P-ABCD的底面ABCD是正方形,PD⊥平面ABCD,E为PB上的点,且2BE=EP.
(2014•广东模拟)如图,四棱锥P-ABCD的底面ABCD是正方形,PD⊥平面ABCD,E为PB上的点,且2BE=EP.