题目内容

已知a为实数，函数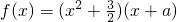 $数学公式$ ，若函数f（x）的图象在某点处存在与x轴平行的切线，则a的取值范围是

A.
$数学公式$
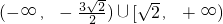
B.
$数学公式$
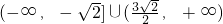
C.
$数学公式$
D.
$数学公式$

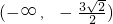
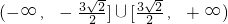
D
分析：若函数f（x）的图象上有与x轴平行的切线，则f'（x）=0有实数解，从而可求a的取值范围．
解答：∵f（x）=x3+ax+ $\text{[math]}$ x+ $\text{[math]}$ a，∴f′（x）=3x2+2ax+ $\text{[math]}$ ，
∵函数f（x）的图象上存在与x轴平行的切线，
∴f'（x）=0有实数解，∴△=4a2-4×3× $\text{[math]}$ ≥0，∴a2≥ $\text{[math]}$ ，解得a≤- $\text{[math]}$ 或a $\text{[math]}$ ，
因此，实数a的取值范围是（-∞，- $\text{[math]}$ ]∪[ $\text{[math]}$ ，+∞），
故选D．
点评：本题主要考查导数的几何意义，考查转化思想、函数与方程思想，解决本题的关键是把问题转化为方程f'（x）=0有实数解．

练习册系列答案

名师面对面同步作业本系列答案

全品小学阅读系列答案

专项训练卷系列答案

必考知识点全程精练系列答案

初中毕业学业考试模拟试卷湖南教育出版社系列答案

畅行课堂系列答案

学习周报系列答案

智能训练练测考系列答案

帮你学小学毕业总复习系列答案

课时导学案天津科学技术出版社系列答案

相关题目

15、已知a为实数，函数f（x）=e^x（x²-ax+a）．
（Ⅰ）求f′（0）的值；
（Ⅱ）若a＞2，求函数f（x）的单调区间．

已知a为实数，函数f（x）=（1+ax）e^x，函数g(x)=

，令函数F（x）=f（x）•g（x）．
（1）若a=1，求函数f（x）的极小值；
（2）当a=-

时，解不等式F（x）＜1；
（3）当a＜0时，求函数F（x）的单调区间．

已知a为实数，函数f(x)=

，g（x）=（1+ax）e^x，记F（x）=f（x）•g（x）．
（1）若函数f（x）在点（0，1）处的切线方程为x+y-1=0，求a的值；
（2）若a=1，求函数g（x）的最小值；
（3）当a=-

时，解不等式F（x）＜1．

（2008•镇江一模）已知a为实数，函数f（x）=x²-2alnx．
（1）求f（x）在[1，+∞）上的最小值g（a）；
（2）若a＞0，试证明：“方程f（x）=2ax有唯一解”的充要条件是“a=

已知a为实数，函数f（x）=（x²+1）（x+a）
（I）若f′（-1）=0，求函数y=f（x）在[-

，1]上的最大值和最小值；
（II）若对于m取任何值，直线y=

x+m都不是函数f（x）图象的切线，求a值的范围．