题目内容
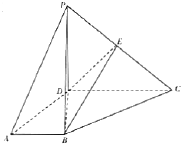 如图,四棱锥P-ABCD的底面为梯形,BA⊥AD,CD⊥AD,PD⊥底面ABCD,PD=AD=AB=1,CD=2AB.E为PC的中点.
如图,四棱锥P-ABCD的底面为梯形,BA⊥AD,CD⊥AD,PD⊥底面ABCD,PD=AD=AB=1,CD=2AB.E为PC的中点.
(I)证明:EB∥平面PAD;
(II)求证:BC⊥平面PBD;
(II)求四面体P-BDE的体积.
解:解:(Ⅰ)证明:取CD中点F,连接EF、BF,又∵PE=EC,据三角形的中位线定理得EF∥PD,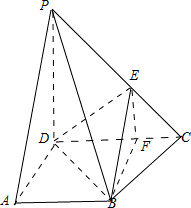
∵EF?平面PAD,AD?平面PAD,∴EF∥平面PAD.
∵AB∥DC,AB=DC= ,∴四边形ABFD是平行四边形,∴BF∥AD,
,∴四边形ABFD是平行四边形,∴BF∥AD,
∵BF?平面PAD,AD?平面PAD,∴BF∥平面PAD.
而BF∩EF=F,∴平面BEF∥平面PAD,
∴BE∥平面PAD.
(Ⅱ)由(Ⅰ)可知:四边形ABFD是平行四边形,AD⊥DC,∴四边形ABFD是矩形,∵AD=1,CD=2AB,
∴DF=FC=FB=1,∴△BCD是Rt△.∴BC⊥BD.
∵PD⊥底面ABCD,∴PD⊥BC,
又∵PD∩AD=D,
∴BC⊥平面PBD.
(Ⅲ)由(Ⅱ)可知:BF⊥DC,PD⊥BF,∴BF⊥平面PCD.
∵PE=EC,∴S△PED= S△PCD=
S△PCD=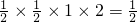 .
.
∴VP-BDE=VB-PED=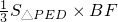 =
=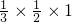 =
= .
.
分析:(Ⅰ)利用三角形的中位线定理和平行四边形的性质是证明线线平行的常用方法之一.如图取CD的中点F,连接EF、FB,可得到EF∥PD,BF∥AD,进而可正得结论.
(Ⅱ)要证明BC⊥平面PBD,只要证明BC垂直于平面PBD内的两条相交直线即可.为此可证明BC⊥PD,及BC⊥BD.要证明PD⊥BC,由已知PD⊥底面ABCD,可证得;由BF=DF=FC,或利用勾股定理即可证明BC⊥BD.
(Ⅲ)由BF⊥平面PCD,把求VP-BDE转化为求VB-PED即可.
点评:本题考查了线线、线面、面面平行和垂直及三棱锥的体积,充分理解和掌握判定和性质是解决问题的关键.

∵EF?平面PAD,AD?平面PAD,∴EF∥平面PAD.
∵AB∥DC,AB=DC=
 ,∴四边形ABFD是平行四边形,∴BF∥AD,
,∴四边形ABFD是平行四边形,∴BF∥AD,∵BF?平面PAD,AD?平面PAD,∴BF∥平面PAD.
而BF∩EF=F,∴平面BEF∥平面PAD,
∴BE∥平面PAD.
(Ⅱ)由(Ⅰ)可知:四边形ABFD是平行四边形,AD⊥DC,∴四边形ABFD是矩形,∵AD=1,CD=2AB,
∴DF=FC=FB=1,∴△BCD是Rt△.∴BC⊥BD.
∵PD⊥底面ABCD,∴PD⊥BC,
又∵PD∩AD=D,
∴BC⊥平面PBD.
(Ⅲ)由(Ⅱ)可知:BF⊥DC,PD⊥BF,∴BF⊥平面PCD.
∵PE=EC,∴S△PED=
 S△PCD=
S△PCD=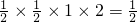 .
.∴VP-BDE=VB-PED=
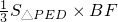 =
=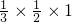 =
= .
.分析:(Ⅰ)利用三角形的中位线定理和平行四边形的性质是证明线线平行的常用方法之一.如图取CD的中点F,连接EF、FB,可得到EF∥PD,BF∥AD,进而可正得结论.
(Ⅱ)要证明BC⊥平面PBD,只要证明BC垂直于平面PBD内的两条相交直线即可.为此可证明BC⊥PD,及BC⊥BD.要证明PD⊥BC,由已知PD⊥底面ABCD,可证得;由BF=DF=FC,或利用勾股定理即可证明BC⊥BD.
(Ⅲ)由BF⊥平面PCD,把求VP-BDE转化为求VB-PED即可.
点评:本题考查了线线、线面、面面平行和垂直及三棱锥的体积,充分理解和掌握判定和性质是解决问题的关键.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=