题目内容
给定椭圆C: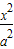 +
+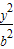 =1(a>b>0),称圆心在坐标原点O,半径为
=1(a>b>0),称圆心在坐标原点O,半径为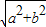 的圆是椭圆C的“伴随圆”. 若椭圆C的一个焦点为F2(
的圆是椭圆C的“伴随圆”. 若椭圆C的一个焦点为F2(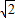 ,0),其短轴上的一个端点到F2距离为
,0),其短轴上的一个端点到F2距离为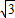 .
.(1)求椭圆C及其“伴随圆”的方程;
(2)若过点P(0,m)(m<0)的直线与椭圆C只有一个公共点,且截椭圆C的“伴随圆”所得的弦长为2
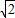 ,求m的值;
,求m的值;(3)过椭圆C的“伴椭圆”上一动点Q作直线l1,l2,使得l1,l2与椭圆C都只有一个公共点,当直线l1,l2都有斜率时,试判断直线l1,l2的斜率之积是否为定值,并说明理由.
【答案】分析:(1)利用椭圆标准方程及其a、b、c的关系即可得出椭圆方程,进而得到“伴椭圆”的方程;
(2)利用点到直线的距离公式、 、及直线与椭圆相切的性质即可得出;
、及直线与椭圆相切的性质即可得出;
(3)利用(2)的结论及点Q的坐标满足“伴椭圆”的方程即可证明.
解答:解:(1)由题意可知: ,a=
,a= ,∴b2=a2-c2=1.
,∴b2=a2-c2=1.
∴椭圆方程为: ,
, ;
;
∴椭圆C的“伴椭圆”方程为:x2+y2=4.
(2)设直线方程为:y=kx+m
∵截椭圆C的“伴随圆”所得的弦长为 ,
,
∴圆心到直线的距离d= ,
,
∵ ,∴d2=2,∴m2=2(1+k2).(*)
,∴d2=2,∴m2=2(1+k2).(*)
又 得(1+3k2)x2+6mkx+3m2-3=0,
得(1+3k2)x2+6mkx+3m2-3=0,
∵直线l与椭圆相切,
∴△=1+3k2-m2=0,
把(*)代入上式得m2=4,∵m<0,解得m=-2.
∴m=-2.
(3)设Q(x,y),直线y-y=k(x-x),
由(2)可知 ,
,
即 ,∴
,∴ ,
,
又∵Q(x,y)在“伴椭圆”上,∴ ,∴
,∴ .
.
∴k1k2=-1为定值.
点评:熟练掌握椭圆标准方程及其a、b、c的关系、点到直线的距离公式、 、及直线与椭圆相切的性质、“伴椭圆”的定义是解题的关键.
、及直线与椭圆相切的性质、“伴椭圆”的定义是解题的关键.
(2)利用点到直线的距离公式、
 、及直线与椭圆相切的性质即可得出;
、及直线与椭圆相切的性质即可得出;(3)利用(2)的结论及点Q的坐标满足“伴椭圆”的方程即可证明.
解答:解:(1)由题意可知:
 ,a=
,a= ,∴b2=a2-c2=1.
,∴b2=a2-c2=1.∴椭圆方程为:
 ,
, ;
;∴椭圆C的“伴椭圆”方程为:x2+y2=4.
(2)设直线方程为:y=kx+m
∵截椭圆C的“伴随圆”所得的弦长为
 ,
,∴圆心到直线的距离d=
 ,
,∵
 ,∴d2=2,∴m2=2(1+k2).(*)
,∴d2=2,∴m2=2(1+k2).(*)又
 得(1+3k2)x2+6mkx+3m2-3=0,
得(1+3k2)x2+6mkx+3m2-3=0,∵直线l与椭圆相切,
∴△=1+3k2-m2=0,
把(*)代入上式得m2=4,∵m<0,解得m=-2.
∴m=-2.
(3)设Q(x,y),直线y-y=k(x-x),
由(2)可知
 ,
,即
 ,∴
,∴ ,
,又∵Q(x,y)在“伴椭圆”上,∴
 ,∴
,∴ .
.∴k1k2=-1为定值.
点评:熟练掌握椭圆标准方程及其a、b、c的关系、点到直线的距离公式、
 、及直线与椭圆相切的性质、“伴椭圆”的定义是解题的关键.
、及直线与椭圆相切的性质、“伴椭圆”的定义是解题的关键. 
练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 +
+ =1(a>b>0),称圆心在坐标原点O,半径为
=1(a>b>0),称圆心在坐标原点O,半径为 的圆是椭圆C的“伴随圆”. 若椭圆C的一个焦点为F2(
的圆是椭圆C的“伴随圆”. 若椭圆C的一个焦点为F2( ,0),其短轴上的一个端点到F2距离为
,0),其短轴上的一个端点到F2距离为 .
.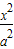 +
+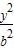 =1(a>b>0),称圆心在坐标原点O,半径为
=1(a>b>0),称圆心在坐标原点O,半径为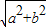 的圆是椭圆C的“伴随圆”. 若椭圆C的一个焦点为F2(
的圆是椭圆C的“伴随圆”. 若椭圆C的一个焦点为F2(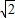 ,0),其短轴上的一个端点到F2距离为
,0),其短轴上的一个端点到F2距离为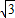 .
.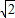 ,求m的值;
,求m的值;