题目内容
已知双曲线
=1的离心率为
，则双曲线的渐近线方程为
- A.y=±
x - B.y=±
x - C.y=±
x - D.y=±
x
A
分析：由e2=
=
可求得a，b之间的关系，从而可求得双曲线的渐近线方程．
解答：∵双曲线的方程为=1，
∴其渐近线方程为y=±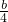
x，
∵离心率为，a2=16
∴e2==，
∴c2=25，
∴b2=9，
∴双曲线的渐近线方程为：y=±x．
故选A．
点评：本题考查双曲线的简单性质，求得a，b之间的关系是关键，属于中档题．
分析：由e2=
=可求得a，b之间的关系，从而可求得双曲线的渐近线方程．解答：∵双曲线的方程为
=1，∴其渐近线方程为y=±
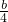x，∵离心率为
，a2=16∴e2=
=，∴c2=25，
∴b2=9，
∴双曲线的渐近线方程为：y=±
x．故选A．
点评：本题考查双曲线的简单性质，求得a，b之间的关系是关键，属于中档题．
练习册系列答案
相关题目
已知双曲线
-
=1（a＞0，b＞0），过其左焦点F1作x轴的垂线交双曲线于A、B两点，若双曲线右顶点在以AB为直径的圆内，则双曲线离心离的取值范围为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、（2，+∞） | ||
| B、（1，2） | ||
C、（
| ||
D、（1，
|
，
分别是双曲线
=1的左右焦点，若以坐标原点O为圆心，
为半径
，则当△
的面积等于
时，双曲线的离心
B.
C.
D.
-
=1（a＞0，b＞0）右焦点且倾斜角为45°的直线与双曲线右支有两个交点，则双曲线的离心离e的取值范围是 ．