题目内容
袋中装有编号为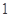 的球
的球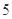 个,编号为
个,编号为 的球
的球 个,这些球的大小完全一样。
个,这些球的大小完全一样。
(1)从中任意取出四个,求剩下的四个球都是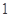 号球的概率;
号球的概率;
(2)从中任意取出三个,记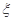 为这三个球的编号之和,求随机变量
为这三个球的编号之和,求随机变量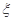 的分布列及其数学期望
的分布列及其数学期望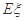 .
.
(1) ;
;
(2) 分布列如下:
3 4 5 6 P 



数学期望为
解析试题分析:(1) 记 “任意取出四个,剩下的四个球都是1号球”为事件A, 则 ,(2)
,(2)  的可能取值有3,4,5,6,则
的可能取值有3,4,5,6,则 ,
, ,
, ,
, ,数学期望
,数学期望 .
.
试题解析:(1)记 “任意取出四个,剩下的四个球都是1号球”为事件A,
则
(2)  的可能取值有3,4,5,6,则
的可能取值有3,4,5,6,则 ,
, ,
, ,
, ,
,
概率分布列如下:
数学期望
3 4 5 6 P 



 .
.
考点:超几何分布的概率分布列与数学期望

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
自驾游从A地到B地有甲乙两条线路,甲线路是A-C-D-B,乙线路是A-E-F-G-H-B,其中CD段,EF段,GH段都是易堵车路段.假设这三条路段堵车与否相互独立.这三条路段的堵车概率及平均堵车时间如表所示.
| | CD段 | EF段 | GH段 |
| 堵车概率 | 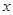 | 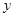 | 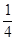 |
| 平均堵车时间 (单位:小时) |  | 2 | 1 |
经调查发现,堵车概率
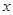 在
在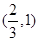 上变化,
上变化,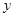 在
在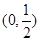 上变化.
上变化.在不堵车的情况下,走甲线路需汽油费500元,走乙线路需汽油费545元.而每堵车1小时,需多花汽油费20元.路政局为了估计
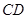 段平均堵车时间,调查了100名走甲线路的司机,得到下表数据.
段平均堵车时间,调查了100名走甲线路的司机,得到下表数据.| 堵车时间(单位:小时) | 频数 |
| [0,1] | 8 |
| (1, 2] | 6 |
| (2, 3] | 38 |
| (3, 4] | 24 |
| (4, 5] | 24 |
(1)求
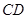 段平均堵车时间
段平均堵车时间 的值;
的值;(2)若只考虑所花汽油费的期望值大小,为了节约,求选择走甲线路的概率.
 内随机取两个数a、b, 则使得函数
内随机取两个数a、b, 则使得函数 有零点的概率为 。
有零点的概率为 。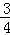 ,求n.
,求n. ,停车付费多于14元的概率为
,停车付费多于14元的概率为 ,求甲停车付费6元的概率;
,求甲停车付费6元的概率;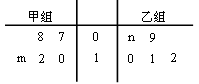
 的值;
的值;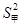 和
和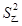 ,
,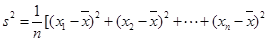 ,
,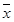 为数据
为数据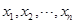 的平均数)
的平均数) 分别为2,3,4,5,现从中任取三条,则以这三条线段为边可以构成三角形的概率是 ▲
分别为2,3,4,5,现从中任取三条,则以这三条线段为边可以构成三角形的概率是 ▲