题目内容
已知函数f(x)=loga(1+x),g(x)=loga(1-x)其中(a>0且a≠1),设h(x)=f(x)-g(x)(1)求函数h(x)的定义域,判断h(x)的奇偶性,并说明理由;
(2)若f(3)=2,求使h(x)<0成立的x的集合;
(3)若
 时,函数h(x)的值域是[0,1],求实数a的取值范围.
时,函数h(x)的值域是[0,1],求实数a的取值范围.
【答案】分析:(1)根据对数函数的真数大于0,可求出函数的定义域,然后根据函数奇偶性的定义进行判定即可;
(2)根据f(3)=2求出a的值,然后解不等式h(x)<0即可求出所求;
(3)研究内函数的单调性,结合讨论外函数的单调性从而求出函数值域,根据函数h(x)的值域是[0,1],可求出实数a的取值范围.
解答:解:(1)定义域为(-1,1)…(2分)
又∵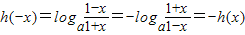
∴函数h(x)为奇函数 …(4分)
(2)∵f(3)=2,解得a=2
∵h(x)<0
∴1+x<1-x⇒x<0
又x∈(-1,1),∴x∈(-1,0)…(8分)
(3)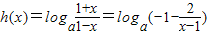
令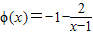 ,
,
可知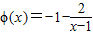 在
在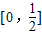 上单调递增,
上单调递增,
因此当a>1时,h(x)在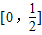 上单调递增
上单调递增
又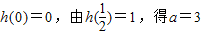 ; …(10分)
; …(10分)
当0<a<1时,h(x)在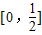 上单调递减,
上单调递减,
由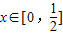 时,函数h(x)的值域是[0,1],
时,函数h(x)的值域是[0,1],
可得h(0)=1与h(0)=0矛盾,所以a∈∅
综上:a=3…(12分)
点评:本题主要考查了对数函数的定义域,以及函数的奇偶性和单调性与值域,同时考查了计算能力和转化的思想,属于中档题.
(2)根据f(3)=2求出a的值,然后解不等式h(x)<0即可求出所求;
(3)研究内函数的单调性,结合讨论外函数的单调性从而求出函数值域,根据函数h(x)的值域是[0,1],可求出实数a的取值范围.
解答:解:(1)定义域为(-1,1)…(2分)
又∵
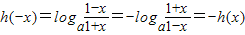
∴函数h(x)为奇函数 …(4分)
(2)∵f(3)=2,解得a=2
∵h(x)<0
∴1+x<1-x⇒x<0
又x∈(-1,1),∴x∈(-1,0)…(8分)
(3)
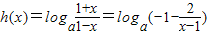
令
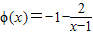 ,
,可知
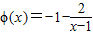 在
在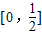 上单调递增,
上单调递增,因此当a>1时,h(x)在
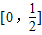 上单调递增
上单调递增又
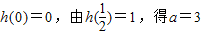 ; …(10分)
; …(10分)当0<a<1时,h(x)在
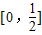 上单调递减,
上单调递减,由
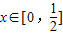 时,函数h(x)的值域是[0,1],
时,函数h(x)的值域是[0,1],可得h(0)=1与h(0)=0矛盾,所以a∈∅
综上:a=3…(12分)
点评:本题主要考查了对数函数的定义域,以及函数的奇偶性和单调性与值域,同时考查了计算能力和转化的思想,属于中档题.

练习册系列答案
相关题目