Question

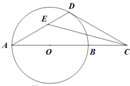（2012•肇庆二模）（选做题）如图，AB的延长线上任取一点C，过C作圆的切线CD，切点为D，∠ACD的平分线交AD于E，则∠CED=

45°

．

Answer 1

分析：连接BD，BD与EC相交于点F，因为CD为圆O的切线，由弦切角定理，则∠A=∠BDC，又CE平分∠ACD，则∠DCE=∠ACE．两式相加∠A+∠ACE=∠BDC+∠DCE．
根据三角形外角定理∠DEF=∠DFE又∠ADB=90°，所以△ADF是等腰直角三角形，所以∠CED=∠DFE=45°．

解答：解：连接BD，BD与EC相交于点F，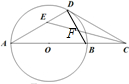
因为CD为圆O的切线，由弦切角定理，则∠A=∠BDC．
又CE平分∠ACD，则∠DCE=∠ACE．
所以∠A+∠ACE=∠BDC+∠DCE．
根据三角形外角定理，∠DEF=∠DFE，
因为AB是圆O的直径，则∠ADB=90°，所以△EFD是等腰直角三角形，
所以∠CED=∠DFE=45°．
故答案为：45°

点评：本题考查有关圆的角的计算．根据图形寻找角的关系，合理进行联系与转化是此类题目的关键．