题目内容
【题目】已知数列
为等差数列，
，
.
（1） 求数列的通项公式;
（2）求数列
的前n项和
.
【答案】（1）
；（2）
.
【解析】试题分析：利用等差数列通项公式列出方程组，求出首项和公差，由此能求出数列
的
通项公式；（2）由（1）可得
，利用错位相减法及等比数列前
项和公式能求出数列
的前n项和
.
试题解析： (1)设数列
的公差为
，依题意得方程组
解得
.
所以的通项公式为
.
（2）由（1）可得，
－得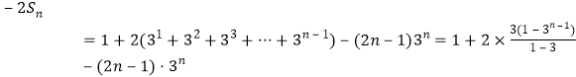
所以
.
【 方法点睛】本题主要考查等差数列的通项公式、等比数列的求和公式以及错位相减法求数列的前 项和，属于中档题.一般地，如果数列是等差数列，
是等比数列，求数列
的前项和时，可采用“错位相减法”求和，一般是和式两边同乘以等比数列的公比，然后作差求解, 在写出“”
与“
” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“
”的表达式.
练习册系列答案
阅读快车系列答案
相关题目
【题目】已知椭圆
＋
＝1(a>b>0)的焦点分别为F1(0，－1)，F2(0,1)，且3a2＝4b2.
(1)求椭圆的方程；
(2)设点P在这个椭圆上，且|PF1|－|PF2|＝1，求∠F1PF2的余弦值．
【题目】通过随机询问72名不同性别的大学生在购买食物时是否看营养说明，得到如下列联表：
男 | 女 | 总计 | ||
读营养说明 | 16 | 28 | 44 | |
不读营养说明 | 20 | 8 | 28 | |
总计 | 36 | 36 | 72 |
(1)根据以上列联表判断，能否在犯错误的概率不超过0.005的前提下认为性别和是否看营养说明有关系呢？
(2)从被询问的28名不读营养说明的大学生中，随机抽取2名学生，求抽到女生人数
的分布列及数学期望.
附：
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
